2015年6月15日更新
割引現在価値の考え方[top]
==== 問題 ===================
小遣いを今年3万円,来年4万円もらう場合と,
今年4万円,来年3万円もらう場合の選択肢が
あった場合,あなたならどっちを選びますか.
それともどちらでも同じですか?
==========================
選択肢(ケータイマクロ問題)
(1)今年3万,来年4万
(2)今年4万,来年3万
(3)どちらでも同じ,差はない
↓
↓
↓
↓
↓
↓
↓
(解説)
ここでのお話のポイントは利子率(金利)が関わって
くることです.
言い換えれば,現在の1万円と1年後の1万円は同じ
価値ではないということです.年の金利を10%
(計算を簡単にするための数値です)として考えましょう.
現在1万円をもっています.金利が10%(複利)と
すると1年後,2年後,・・,n年後の元利合計は
次のようになります.
1年後=1×(1+0.1)
2年後={1×(1+0.1)}×(1+0.1)
=1×(1+0.1)^2
3年後=1×(1+0.1)^3
n年後=1×(1+0.1)^n
上の関係を逆に見ると,1年後の1.1万円は今年の
1万円と同等であり,2年後の1.21万円は今年の
1万円と同等の価値があるということになります.
これらから,将来上がる収益を現在時点ではいくらに
なるかを計算するには,将来の各時点での収益を,
1年後なら(1+金利),
2年後なら(1+金利)^2,
n年後なら(1+金利)^nで
割ってやればよいということになります.
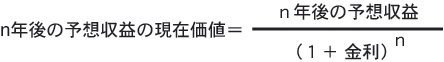
これが将来の予想収益を現在時点の価値に評価する
「現在価値法」の基本的な考え方です.
例えば,3年後までの予想収益の流れの現在価値の合計
は次のようになります.
予想収益の総額=1年後の収益/(1+金利)
+2年後の収益/(1+金利)^2
+3年後の収益/(1+金利)^3
【問題の解答】
先ほどの小遣いの例に戻って,現在価値法の考え方を
適用すると,次のようになります.
小遣いを今年3万円,来年4万円の場合の現在価値:
4
3 + -------------- = 3 + 3.6 =6.6万円
1+0.1
小遣いを今年4万円,来年3万円の場合の現在価値:
3
4 + -------------- = 4 + 2.7 =6.7万円
1+0.1
結局,今年4万円,来年3万円もらった方が,現在価値
は高いということになります.
この現在価値法の計算は,「収益還元法」とも呼ばれ
将来資産の価値を測る場合に様々な分野で利用されてい
ます.例えば,土地の評価,貸しビルの評価,ローンの
計算,裁判の賠償額の計算などに使われています.
経済学の教科書では,投資を評価するときの
「投資の限界効率」や債券の市場価格を計算する場合
などに登場します.
★補足情報 -------------------------------------------
上で使用した「小遣いの例」は,中国の有名な故事成語,
「朝三暮四(ちょうさんぼし)」をヒントに作成しました.
「朝三暮四」を知らない方は,以下の私のメールマガジンを
参照してください.割引現在価値法と等比数列の基本的な考え方
について学ぶことができます.
投資の限界効率[top]
ここで学ぶ投資(investment)は,消費者によるいわゆる
「株式投資」ではなく,企業による投資活動,設備投資
が主な対象です.GDPの約15%を占めるのがこの投資
です.設備投資とは,具体的には工場を建設したり,
機械などの設備を購入あるいは更新したりする投資のこと
です.
「投資は利子率の減少関数になる,すなわち,利子率
が下がれば投資は増加する.利子率が上がれば投資は
低下する」という投資の限界効率の考え方を学びます.
企業は投資を決定するとき,どのような要因を考慮する
でしょうか.将来の景気の見通し(予想)が重要な要因
になることはいうまでもありません.将来の予想を所与
とした場合,次の2点がポイントとなります.
1.投資から得られることが予想される将来の収益の
現在価値
2.投資のコスト
投資からの収益の方がそのコストより大きいと判断され
れば,その投資は実行することが決定されます.
逆であれば,その投資は見送られます.この点を正確に
定式化してみよう.
[記号説明]
C:機械(投資)の費用
n:機械の経済的耐用年数
Rt :t期の投資の予想収益
r :利子率
ρ:投資の限界効率(marginal efficiency of the investment)
将来発生する収益を現在時点で評価する考え方を
「割引現在価値法」(Present Discounted Value Method)
と呼んでいます.
投資を実行した場合,収益はその後何年かにわたって
発生することが予想されます.
その予想収益を現在時点で評価して,収益がコストを
上回れば投資を実行する価値があることになります.
予想収益の流列は次のようになります.
R1,R2,R3,・・・・・,Rn
予想収益は将来時点の値であり,現在の投資コストと
比較するためには,将来発生するであろう収益を現在
時点の値に評価する必要があります.
まず次のような簡単な例を使って説明しておきましょう.
1万円を年10%の複利で銀行に預金する場合を考えて
みましょう.
2年後までを計算すると次のようになります.
10,000 円 → 11,000 円 → 12,100 円
(現在) (1年後) (2年後)
1×(1+0.1)=1.1 {1×(1+0.1)}(1+0.1)
=1×(1+0.1)^2
現在の1万円は1年後には11000円になるので,現在の
1万円は1年後の11000円と同等の価値があるとみなす
ことができます.これを逆に考えれば,1年後の11000円
は現在の1万円と同等であるといえます.
1年後の11000円から1万円を計算するには,
(1 + 利子率)で1年後の収益を割ります.
2年後の収益の現在価値は予想収益を(1+割引率)^2
で割ればよいことになります.従って一般に,
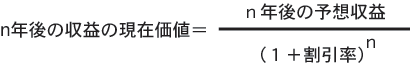 (1)
(1)
n年後までの投資から得られる将来の予想収益全体の
現在価値Vは次のようにかくことができます.
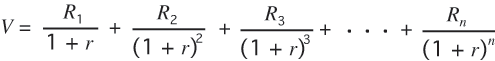 (2)
(2)
上の式で毎期の予想収益が一定(R)でしかもそれが無限
に続くと仮定すると,初項がR/(1+r),公比が1/(1+r)の
無限等比数列となり,現在価値の合計は次のようになります.
ここで,無限等比数列の和の公式を使っています.
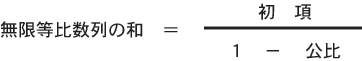
上の式にあてはめて計算すると,
![]() (3)
(3)
一方,投資の費用Cと等しくさせる将来の予想収益の
現在価値の割引率(予想収益率)ρ(ロー)のことを,
「投資の限界効率」(marginal efficiency of the investment)
と定義します.
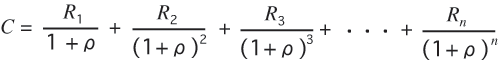 (4)
(4)
投資収益と投資費用の比較によりその投資が採用されるか
否かが決定されます.
V >C ならば (あるいはρ> r)その投資計画は採用され,
逆ならば採用されません.
投資収益と投資費用の比較によりその投資が採用されるか
否かが決定されます.
V > C → ρ> r → 投資採用
V = C → ρ= r → 少なくとも損失なし
V < C → ρ< r → 投資不採用
その投資が採用されるかどうかは,市場利子率と投資の
限界効率の大小関係に依存することがわかります.
投資の限界効率の高い投資プロジェクトから順に採用さ
れていき,限界効率の悪いもの程採用の序列は低くなります.
市場利子率と等しい限界効率の投資が採用の臨界点です.
これより小さい限界効率の投資は採用されません.
この関係を図に描いたのが投資の限界効率表です.
投資の限界効率表
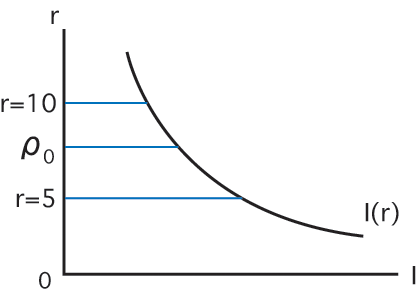
市場利子率が10%ならば,ρoの限界効率の投資は採用
されませんが,利子率が5%ならば,この投資プロジェクト
は採用されます.従って,利子率が低下するほど投資は
増大することがわかります.利子率が上昇すれば,より
高い限界効率の投資しか実行されません.逆に,利子率
が低下すれば低い限界効率の投資でも実行することができます.
すなわち,「投資は利子率の減少関数である」ということ
が明らかになりました.これがケインズによる投資の
限界効率の考え方です.
-----------------------------------------------
■投資の限界効率を求める例題
-----------------------------------------------
「笑天商店」はプロ野球球団に50億円投資する
プロジェクトを計画中である.このプロジェクト
からは毎年4億円の収益が10年間にわたって得ら
れると想定されています.
1.投資の限界効率をρとして,投資の限界効率の
定義を表す式をたてなさい.
2.期間を無限とみなした上で,無限等比数列の和
の公式を使って,投資の限界効率ρを求めなさい.
3.投資資金を借りるときの金利が5%であったとき,
この投資プロジェクトは採用すべきかどうかを
判断しなさい.
-----------------------------------------------
(解説)
投資の限界効率の定義(上の(4)式)から,
例題は次のように整理することができます.
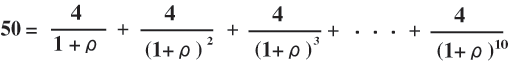 (5)
(5)
上式を満たすρが投資の限界効率.
(なお,表計算ソフト(エクセル)などを使うと,上の式
に基づいてρを簡単に計算することができます.)
期間を無限にすると,無限等比数列の和の公式が使えます.
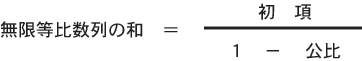
(5)式の右辺にこの公式を適用すると,(5)式は
次のようになります.
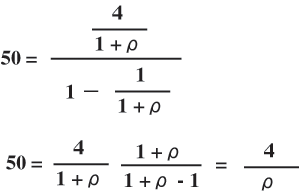
これより,ρ=0.08 すなわち,
投資の限界効率は8%.
投資資金を5%の金利で借りても,投資の限界効率
は8%なので利益がでることが予想されるので,
この投資プロジェクトは採用されます.
ケータイマクロ問題[top]
----------------------------------------
■さらに,練習問題
----------------------------------------
(設問1)ある投資プロジェクトの費用は10億円で、
このプロジェクトからは、毎年1億円の収益が10年間に
わたってあがる。期間を無限とした場合、投資の限界効率
はいくらになるか。
三者択一問題
(1) 0.1
(2) 0.2
(3) 0.3
(設問2)上の投資プロジェクトが採用されるためには,
費用を借りるときの金利水準は次のどの場合か.
三者択一問題
(1) 12%
(2) 11%
(3) 9%
その他の投資理論[top]
1.加速度原理
2.資本ストック調整原理
3.利潤原理
4.新古典派投資理論
5.トービンのq理論(James Tobinの写真,写真2)
■加速度原理
望ましい資本ストックと実際の資本ストックとの差を
1期で埋めるように今期の投資を行うと想定するのが
加速度原理です.
1.資本ストックKと産出高Yの間には資本係数vを媒介
として一定の関係があります.資本係数とは,産出
量1単位を得るのに必要な資本ストックの量のことです.
2.今期の投資を It,今期の資本ストックをKt,1期前
の期末の実際の資本ストックを Kt-1 とかくと,今期
の投資は今期の資本ストックを達成するために行う
ものですから,次のようにかけます.
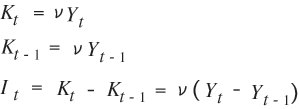
結局,投資は所得の増加分に比例するという関係が得
られます.これが加速度原理です.
■資本ストック調整原理
望ましい資本ストック(K*)と現実の資本ストックとの
乖離をある一定割合だけ毎期毎期埋めていくように投資を
実行し,数期間をかけて望ましい資本ストックに到達しよ
うとするのが,資本ストック調整原理です.加速度原理
では差を一気に埋めてしまいます.
![]()
政府の経済(経済財政)白書などではこのタイプの投資
関数の推定がよく行われています.なお,加速度原理と
共に資本ストック調整原理では,資本係数は固定されています.
■利潤原理
投資は所得水準に依存するというのが利潤原理の投資
関数です.投資が行なわれるには企業側に利潤が発生
していなければなりません.その利潤は,企業の生産高
すなわち所得水準によって決まると考えます.
■新古典派投資理論
加速度原理や資本ストック調整原理では,資本係数は
固定されていました.これに対して,新古典派投資理論
は生産要素間の代替を認めます.ジョーゲンソン(1965)
は,資本ストックと労働の間で代替の可能性を許す生産
関数を前提として,最適な資本ストックの水準を企業の
利潤極大化行動から求めました.企業の最適化行動から
望ましい資本ストックを求め,次に望ましい資本ストック
と現実の資本ストックとの乖離は分布ラグに基づいて埋め
られていくと想定して,投資関数を導出します.
ジョーゲンソンの投資関数は,資本ストック調整原理を
一般化,理論的に精緻化し,実証分析にも耐えられるもの
として評価されています.
■トービンのq理論
トービンのqは次のように定義されます.

企業の市場価値は株式市場で決まる株価に反映される
とみなします.また,株価は企業の将来にわたる収益
力を反映したものであると考えます.qが1以上の場
合は,企業が投資を1単位追加的に行うとき,それに
要する費用(買い換え費用)よりもそこから得られる
予想利益(株式市場での株価に表れると考える)の方
が大きいので,この投資を行うことになります.qが
1以下の場合は,市場が評価する企業の価値は現存す
る資本ストックの価値より小さいので,現存の資本ス
トックは過大であることになり,投資は控えます.
投資はqの増加関数になるというのが結論.
メールマガジン[top]
等比数列と現在価値法の基本的な考え方については,
以下の私のメールマガジンを参照してください.
株式市場については次のメールマガジンを参照してください.