2014年11月10日更新
事後的関係(ex post):恒等式.国民所得の定義
事前的関係(ex ante):
計画された段階で,需要と供給が等しくなること.
その条件を満たす所得水準を均衡所得という.
均衡(equilibrium)とは事前的な概念であることに注意しよう.
国民所得の決定とは,上の意味での均衡所得を求めることです.
限界消費性向[top]
【簡単なアンケート,ケータイマクロ,五者択一】------------
あなたの今月のバイト代は,先月に比べて1万円増加したとします.
この増加した1万円をあなたはどのように使いますか?
答としては,例えば,
1 増えた1万円分は全部使ってしまう.
2 増えた1万円分は使わずにすべて貯蓄にまわす.
3 増えた1万円分のうち,3000円ぐらいは使う.
4 増えた1万円分のうち,5000円ぐらいは使う.
5 増えた1万円分のうち,7000円ぐらいは使う.
あなたは,一番どれに近いですか?
--------------------------------------------------------------
今回から,
限界消費性向(MPC: Marginal Propensity to Consume)
という重要な概念が登場します.ぜひこの概念を理解してください.
マクロ経済学で使用する限界消費性向は,一人一人の
限界消費性向ではなく,経済全体(マクロ経済)での値です.
上のアンケートで,
1 と答えた方の限界消費性向は1
2 と答えた方の限界消費性向は 0
3 と答えた方の限界消費性向は 0.3
4 と答えた方の限界消費性向は 0.5
5 と答えた方の限界消費性向は 0.7
限界消費性向は,経済全体での値ですから,MPC = 1,や
MPC = 0 はありえません.
なぜなら,すべての人が所得増加分を全部使い切るとか,
まったく使わないということはありえないからです.
従って,
0 < 限界消費性向 < 1
となるのです.
消費の増加分
限界消費性向 = -------------------
所得の増加分
言い換えれば,限界消費性向とは,所得の増加分のうち
消費に振り向ける部分の割合のことです.
単純なモデル[top]
経済モデルの考え方に慣れよう.
経済の支出面からは,消費(C),投資(I),政府(G),
輸出(EX),輸入(IM)
があるが,最も単純なC とI だけからなる経済を考えよう.
消費は,主として所得水準に依存して決まると考えられます.
消費は所得水準の上昇と共に増加します.
この関係を消費関数と呼びます.
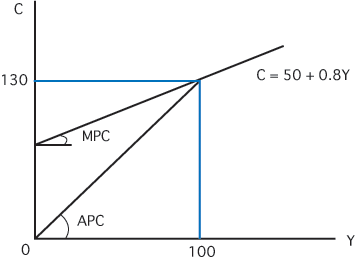
消費関数 C=Co +cY
1つの例として C=50+0.8Y
Co(=50):基礎消費(独立的消費)
c :限界消費性向(MPC: Marginal Propensity to
Consume=0.8)
●限界消費性向は,所得が1単位増加したとき,
それから消費に振り向ける割合を示します.
例えば,MPC=0.8なら所得が1兆円増加すると,
消費は0.8兆円増加します.
「限界(marginal)」という言葉は,経済学では「増加分」
を意味します.
限界消費性向は,その定義から 0 < MPC < 1 の範囲をとります.
●平均消費性向(APC: Average Propensity to Consume)は
消費額全体を所得額全体で割った値で,
所得に占める消費の割合を表します.
APC= C/Y = Co/Y + c
平均消費性向は,所得が増加するにつれて低下します.
そのかわり,平均貯蓄性向(貯蓄/所得)は増加します.
以下の図でも確認しましょう.
上のような線形の消費関数を前提にすると,
MPC < APC の関係があります.
消費関数

投資はある一定の値が最初から与えられているものとします(所与).
所得の決定とは以下の式を満たす所得水準を求めることです.
総生産(=総所得)=総需要
いま,需要が消費と投資だけからなる単純なケースを考えて
いるので,総生産をYで表すと,経済モデルは以下の
3本の方程式から構成されます.
経済モデル[top]
財市場の均衡式 Y= C + I (1)
消費関数 C = Co + c Y (2)
投資支出 I = Io (3)
(解き方)
(2)と(3)を(1)に代入し,Yについて解きます.
Y = C + I
= (Co + c Y ) + Io
Yについて整理,
(1 - c) Y = Co + Io
これから,
![]() (4)
(4)
(4)が均衡所得を表し,
1/(1-c)を乗数(multiplier)と呼びます.
45度線図[top]
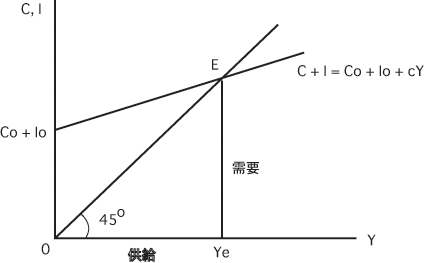
横軸に所得(供給),縦軸に消費と投資(需要)をとります.
直角二等辺三角形OEYeに注目します.
需要の合計線C+Iが45度線を切る点Eでは,
需要=供給の条件が満たされています.
均衡の安定性[top]
決定された均衡所得が安定な均衡の上にあるかどうかが大切です.
もし均衡が不安定なら,均衡所得は一時的なものであり,
その重要性は弱まるからです.
均衡の安定性をチェックしてみましょう.
均衡の安定性チェック
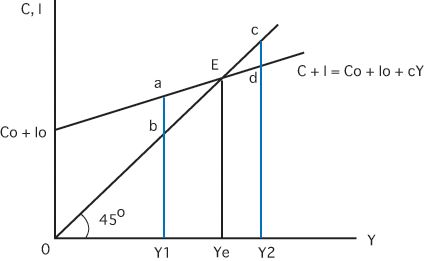
均衡が安定であるか否かを判定するには,所得が均衡から
少し離れたとき,均衡所得へ戻る力がモデルに内在して
いるかどうかによります.
Y = Y1 のとき:
需要>供給(abの超過需要)→意図しない在庫の減少
→生産計画拡大→Y増加
Y = Y2 のとき:
需要<供給(cdの超過供給)→意図しない在庫の増加
→生産計画縮小→Y減少
いずれの場合でも,均衡Eは安定です.
貯蓄投資バランス図[top]
貯蓄関数の導出
貯蓄は,所得から消費を差し引いたものと等しくなります.
S = Y - C
= Y - Co - c Y
= ( 1 - c ) Y - Co
45度線と消費関数の差を下側の図に移してやれば,
貯蓄が得られます.
貯蓄関数に投資関数を重ね合わせます.
投資は自立的投資だけからなっているので,ある水準で
水平になります.
貯蓄関数と投資関数の交点Eで,均衡所得水準が決定されます.
以下の図では上の部分が45度線図,下が貯蓄投資図であり,
両者の均衡点Eは一致します.
貯蓄投資バランス図(下の図)

ケータイマクロ問題[top]
【問題1】マクロ経済モデルが次のように与えられています.
財市場の均衡式 Y= C + I (1)
消費関数 C = 10 + 0.8 Y (2)
投資支出 I = 20 (3)
このとき,均衡所得(GDP)は次のどれでしょう.
単位は兆円
1 150
2 375
3 500
【問題2】消費関数C=Co + c Yについて,以下の記述で
誤りはどれか.
1.Coは基礎消費といい,Co>0である.
2.cは限界消費性向といい,0<c<1である.
3.消費関数の傾きは1以上になる.
インフレギャップ・デフレギャップ[top]
上で求めた均衡所得は,財市場を均衡させる(需要=供給)
所得水準ではありますが,
労働市場を均衡させる「完全雇用所得」
(full employment income)とは限りません.
完全雇用所得とは,働きたい人はすべて雇用されている
状態に対応する所得水準のことです.
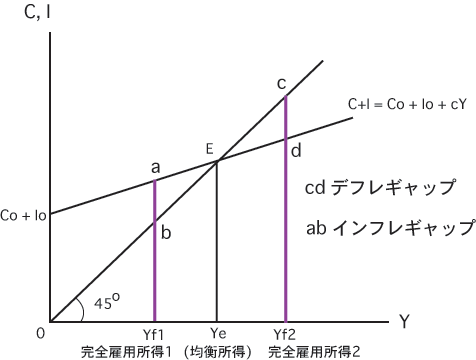
完全雇用所得がYf1のとき:ab の慢性的な超過需要の存在 →
→インフレーションの発生.需要を抑制することでYf1達成可能
完全雇用所得がYf2のとき:cd の需要不足 →
→需要拡大政策により完全雇用Yf2を達成可能
(注意)デフレギャップ,インフレギャップをYeとYf2,
あるいは,YeとYf1との差と誤解することがよくあるので
注意してください.
(関連事項)
2007.05.28(月) 内閣府,2007年1-3月期需給ギャップはプラス0.7%,
10年ぶりに2四半期連続でプラス(需要>供給)
関連新聞記事[top]
均衡の安定性の項で生産の調整プロセスを説明しましたが,新聞記事では
以下のような記述を見つけることができました.
○「在庫率,23年ぶり高水準.4月3%上昇.景気循環鮮明に」
日経1998年5月28日,夕刊
「景気の低迷が長引く中で「個人消費の落ち込み→在庫の積み増し→生産抑制」
の悪循環が鮮明になっている.通産省が28日発表した4月の鉱工業生産動向速報
によると,在庫率指数(95年=100,季節調整済み)は前月に比べて3.0%上昇,
第1次石油ショック後の75年1月以来の高水準となった.」
●貯蓄率に関したニュース
「日米欧の家計で貯蓄率が低下,米国はユーロ圏の1/4」(朝日新聞,2004年6月10日)
欧州中央銀行(ECB)と経済協力開発機構(OECD)の共同調査.
欧州中銀のウェブサイトで公表された調査では,3つの地域の貯蓄率は90年代を通して低下.
2002年 1991年
ユーロ圏 9.6% 13.8%
米 国 2.4% 7.5%
日 本 5.2% 13.8%
European Central Bank(欧州中央銀行):
http://www.ecb.int/press/04/pr040609.htm
(June 9, 2004)
http://www.ecb.int/pub/pdf/comparisonhouseholdsavingseuusjpnen.pdf
(8pages)
●チャールズ・Y.ホリオカ「貯蓄率と高齢化(1)〜(8)」
『日本経済新聞』やさしい経済学,2004年9月9日〜9月21日
日本の場合ライフサイクル仮説が妥当し,高齢化に伴い貯蓄率が低下していることを指摘しています.
日経テレコン21で記事検索[top]
平均消費性向の最近の値はどのくらいであるかを,
「日経テレコン21」を使って調べてみましょう.
「記事検索」で「平均消費性向」とキーワード入力して
検索すると,この言葉を含む記事を探し出してくれます.
総務省の発表として,いくつか記事が見つかります.
2002年の平均消費性向は約0.73です.
新聞のニュースソースは以下の総務省発表の統計です.
総務省,家計調査報告(2003年4月25日公表):
http://www.stat.go.jp/data/kakei/sokuhou/kin/index.htm
http://www.stat.go.jp/data/kakei/sokuhou/kin/zuhyou/056b_t1.xls
(エクセルファイル)
付録A:高校数学の復習[top]
GDPの決定では,いくつかの基礎的な数学を使っています.
復習しておきましょう.
1.一次関数の性質
消費関数C = Co + cY は一次関数の形をとっています.
一次関数は次の性質があります.
(★)切片と傾きが決まれば直線の式(一次関数)は
1つ決まる.
ここで,
切片はCo(基礎消費),
傾きはc(限界消費性向)です.
消費関数では,Co>0,0<c<1の条件がつきます.
消費関数では,所得(Y)が増加すれば消費(C)は比例的に
増加します.
横軸にY,縦軸にCをとると,
C = Co + cYは右上がりの直線として描かれます.
2.直角2等辺3角形の性質
45度線図で,供給(Y)=需要(C+I) を明らかにするとき,
直角2等辺三角形の性質を使っています.
付録B:エクセルファイル[top]
表計算ソフトエクセルを活用すると,GDPの決定プロセスを
シミュレートすることができます.
以下のファイルをダウンロードしてエクセルファイルを
開いてみてください.
GDPの決定と45度線図の描き方が学ぶことができます.
より詳細は私の『マッキントッシュで経済学』(日本評論社)第7章を参照してください.
DetermGDP.xls (エクセルファイル)
付録C:Mathematica プログラム[top]
1.単純なマクロ経済モデルを,連立方程式として解くことができます.
財市場の均衡式 Y= C + I (1)
消費関数 C = Co + c Y (2)
投資支出 I = Io (3)
上のモデルを数式処理ソフト Mathematica で記述して解くと次のようになります.プログラム部分は太字で書きます.Mathematica の記号制約から C, I は使えないので次のようにしています.
model = {
y == con + inv,
con == con0 + mpc*y,
inv == inv0
};
kai = Solve[model, {con, inv, y}]
答えは,
{{ con -> -(con0 + inv0*mpc)/(-1+ mpc) , y -> -(con0 + inv0)/(-1 + mpc), inv -> inv0}}
数値解を求めるには,
kai /. {con0 -> 10, inv0 -> 20, mpc -> 0.8}
答えは,
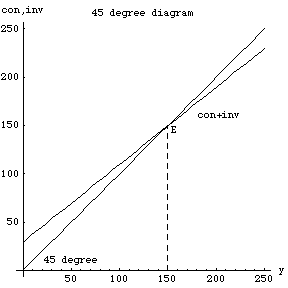
{{con -> 130., y -> 150., inv -> 20}}
2.45度線図を描く
(* ----------------------------------------
*)
(* simple model : GDP and 45 degree diagram *)
(* -----------------------------------------*)
con0 = 10;
inv0 = 20;
mpc = 0.8;
model2 = {
y == con + inv,
con == con0 + mpc y,
inv == inv0
};
suchikai = Solve[model2, {con, inv, y}];
ye = Part[y /. suchikai, 1]
(* -------------------------------- *)
(* 45 degree diagram *)
(* ---------------------------------*)
juyo[y_] := con0 + inv0 + mpc y;
Plot[
{juyo[y], y}, {y, 0, ye + 100},
AspectRatio -> Automatic,
AxesLabel -> {"y", "con,inv"},
PlotLabel -> "45 degree diagram",
Epilog -> {
Text["E", {ye + 7, ye - 5}],
Text["con+inv",
{ye + 30, ye + 10}, {-1, 0}],
Text["45 degree", {20, 10}, {-1, 0}],
Dashing[{0.02}],
Line[{{ye, 0}, {ye, ye}}],
Line[{{ye , 0}, {ye, ye}}]
}
]
上のプログラムを実行すると,次の図が得られます.