パソコンソフト活用の極意

笹山　茂「パソコンソフト活用の極意」　『電脳経済学のススメ：超・入門経済学1997　経済セミナー増刊』　日本評論社　1997年４月，pp.40-46．

（同書には，その他経済学に役立つインターネットのサイトの紹介をはじめとして，経済学の各分野の学び方の指南書ともなっています．新入生はもちろんのこと上級生にも十分役立つ情報が満載されていますので是非参照を勧めます．）

パソコン活用でどう変わる

　朝一番に私がすることは，自動化された通信ソフトを起動してニフティーサーブにアクセスし，メールやインターネットウォッチの記事，さらにいくつかのフォーラムの記事にざっと目を通すことです．通信ソフトは一度設定してしまえば後は全くの自動運転で，アクセスから終了まで勝手にやってくれます．メール等は後でまとめて読むことができます．その後，PPP接続で大学のメールサーバにアクセスして，大学のアドレスに届いたメールをチェックします．ついでにネットニュースやウォールストリートジャーナルのWebサイトにアクセスし，ニュースに目を通します．時間に余裕がないときは，目ぼしい記事をダウンロードして後で読みます．その後，エクセルを起動して，日経新聞の為替欄から前日の為替レートを入力して毎日の動きを注視します．為替の入力はパソコンを購入してからの習慣になっているので，10年以上は続いているでしょう．講義ノートもノートパソコンの中です．教室にノートパソコンを持ち込めばプリンアウトしたノートは不要となり，講義ノートの修正もすぐできます．時には，教室内の情報コンセントからインターネットや学内のパソコン通信網にアクセスしてプレゼンテーションしたりもします．このような私のシステムも一朝一夕に出来上がったわけではなく，幾多の試行錯誤を経て現在のようになってきました．講義ノート以外にもこれまで発表した著作や論文から住所録まで，私の知的財産がノートパソコンの中に凝縮されています．ニコラス・ネグロポンテが，とある企業の受付嬢に彼のノートパソコンの評価を問われて「100万ドルから200万ドルの間」と答えた気持ちがよくわかります（『ビーイング・デジタル』アスキー，1995年，22ページ）．従って，パソコンが故障したら一大事です．データのバックアップは毎日行っています．さらに，私の場合はデスクトップパソコンが予備のサブマシンとなっており，ノートパソコンがダウンした場合でも，仕事が中断しないような工夫をしています．
　パソコンは今や経済学を学ぶ者にとっての道具箱となっています．昔は集計用紙にデータを書き写し電卓をたたいて増加率を計算したり，グラフ用紙の升目を数えながら折れ線グラフを描いたり，簡単な回帰分析のために汎用コンピュータ用の穿孔カードを一杯抱えていましたが，これらは今となっては昔話．パソコンは私たちの必需品となっています．これは世の中が進歩すればどの世界でも起こる出来事です．もし暇があれば街中の建築現場を覗いてごらんなさい．今どきのこぎり，釘と金槌で家を建てている大工さんなんかいません．大工さんの道具は今ではすべて電動工具です．学問の世界だけが古色蒼然としたスタイルのままでいいはずはありません．パソコンを積極的に利用して効率よくかつ楽しく経済学を学ぼうではありませんか．

７つ道具

　パソコンのソフトにはたくさんの種類がありますが，経済学を学ぶ者としていったいどれを使いこなせるようになればいいのでしょうか．今ではこれぐらいをマスターしていれば大丈夫というおおよその目安があります．ワープロ，通信（パソコン通信，電子メール，インターネット），表計算，グラフィックス，データベース，プレゼンテーションの各ソフトを一通り使えるようになれば取り敢えず今のところは大丈夫です．こんなにたくさん学ばなければならないのかと溜息をつく人がいるかもしれませんが，必要がでてきたら始めればよいのです．最初から全部マスターしようと意気込むと息切れしてしまいます．パソコンは今ではウインドウズとマックの２つの系列に整理されて，代表的なソフトウェアは両方に対応していますので，主にそのようなソフトを対象にして紹介しましょう．
　ワープロは何をするにしても基本です．キーボードを見ないで両手で入力するタッチタイピングをできればマスターして欲しいものです．論文をまとめるという観点からすれば，脚注，目次作成，索引，アウトライン作成機能がついたワープロが好ましいでしょう．さらに，経済学では数式を多用するので，数式を簡単に作成できる機能を備えていることも重要です．マイクロソフトワードと一太郎がワープロの２大ブランドですが，英文ワープロとしても使おうとすれば米国生まれの前者の方が有利かもしれません．インターネットの爆発的な拡散によってメジャーな存在にのし上がった通信ですが，電子メール（E-mail）のアドレスを１つ持つだけで全世界の人々を相手にすることができるという大きな御利益があります．ネットスケープナビゲーターかインターネットエクスプローラーを使えば世界中のウェブページをネットサーフすることができます．インターネット上のサーチエンジンを使って上手に検索すればかなりの確度で自分の目的に合った情報を入手することができます．表計算は地味ですが，経済学部の学生必携のソフトウェアです．電卓並の計算から表の作成，統計分析までこなせる経済学にはなくてはならないソフトで，マイクロソフトエクセルとロータス1-2-3が双璧をなしています．表計算については次節で特に詳しく説明します．経済学はよく図を使う学問です．無差別曲線，費用曲線，IS-LM曲線等々の図が登場します．論文を作成するとき，図だけ手書きというのでは興ざめです．是非きれいな曲線をパソコンで描きたいものです．そのような目的に最適なのがアドビイラストレーターです．数値データを管理するには表計算の方が便利ですが，住所録や文献の整理にはデータベースソフトの方に一日の長があります．ファイルメーカーProが代表的ソフトです．ただ，データベースはほどほどに作るのがコツです．整理するのに没頭してしまうと，研究のためのデータベースではなく，整理のために整理しているということになりかねませんので．ゼミで発表する場合は，資料（ハンドアウト）を配付して行うというのが一般的でしょうが，設備が揃っていれば，ノートパソコンを持ち込み直接パソコンの画面をプロジェクターで拡大投影して発表することも可能です．そのような目的に使用するのがプレゼンテーションソフトです．代表的なものにパワーポイントがあります．最近は学会でもこの手のソフトでの発表が増えつつあります．企業では顧客に対する説明の際に積極的に利用されています．なお，個々のソフトをすべて揃えるとなると大変ですが，クラリスワークスなどのように，１つのソフトでワープロから通信までほとんどまかなえる統合型ソフトもありますから，これから始めるというのも一つの賢明な方法です．

表計算の極意

　クリントン米大統領は，「誰もが8才で読むことができ，12才でインターネットにログオンできて，18才で大学に入学でき，すべての成人は生涯学ぶことができる」（1997年2月4日の一般教書演説）ことを教育の目標に掲げましたが，表計算ソフトを使いこなせることが経済学部の学生にとっての目標と言っても過言ではありません．様々なパソコンソフトの中で，経済学を学ぶ者にとって最も重要でかつ最も役立つのはエクセルやロータス1-2-3のような表計算ソフト（英語ではスプレッドシートspreadsheet）でしょう．最近の表計算ソフトは計算するだけでなく，グラフの作成はもちろんのこと，簡単な作図機能，様々な内蔵関数，データベース機能，マクロと呼ばれる手続き型のプログラミング機能を備えているので，平均を求めるような簡単な計算から基本的な回帰分析までかなりのことがこなせてしまうのです．表計算ソフトを一通り使いこなせれば経済学部の学生として一人前といってよいでしょう．ここでは，表計算ソフトエクセルを使って，経済学で出会う例を挙げながら簡単に説明しましょう．表計算ってこんなふうにも使えるんだと納得してもらえれば望外の喜びです．
　最初に，「金利が複利で年5.6%，返済期間が20年で1000万円を借り入れたとき，毎月の返済額はいくらか」という問題を考えてみましょう．このときの基本的な考え方は，毎月の返済額の現在価値の合計が借入金に等しくなるように毎月の返済額が決められるということです．現在価値というのは，将来の返済額を現在で評価したらいくらに相当するかを計算する概念で，投資の限界効率の計算等経済学ではよく登場します．借入金をＬ円，借入期間をｎカ月とし，月利をｒとします．このとき毎月の返済額ｘは次の式から求められます．
　　　
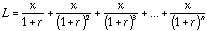
みなさんが高校で学んだ等比級数の公式を使えば，
　　　
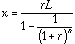
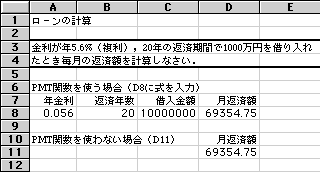
となります．表計算（図１参照）ではD11の場所に =(A8/12)*C8/(1-1/(1+A8/12)^(B8*12)) と打ち込めば，69354.75（円）と表示されます．これが毎月の返済額です．少し面倒ですが，計算の原理を学ぶ上では非常に重要なことです．原理を理解した後は，表計算に内蔵されているPMT関数を使うと簡単に計算できてしまいます．D8の場所に=PMT(A8/12,B8*12,-C8)と入れればよいのです．同じ結果が表示されます．

　　　　　　図１　ローンの計算


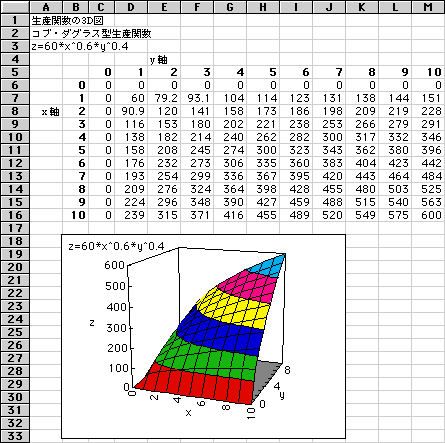
　２つ目の例は，ミクロ経済学で登場する生産関数の例です（図２参照）．私の過去の経験からしてもいきなり生産関数とか等量曲線とかいわれてもなかなかイメージがつかみにくいものです．このようなときに表計算の計算機能とグラフ機能を利用すると明快になる場合があります．コブ・ダグラス型生産関数としてz=60*x^0.6*y^0.4 が与えられたとき，どんな形をしているかをすぐに想像できる人がどれほどいるでしょうか．与えられた式に則って，x とy の数値を0から順次増やしていけばz の値が求まります．x，y，z の関係を３次元のグラフに描けば生産関数の立体図が得られるはずです．図２でC6には=60*B6^0.6*$C$5^0.4 と入力されています．以下同様にしてz の値を計算することができます．B5からM16の長方形の範囲を選択して３Dグラフを選べば図のような生産関数が得られます．こんな形をしていたのですね，コブ・ダグラス型は．なお，エクセルではこの３D図を回転させて様々な視点から眺めることもできます．

　　　　　　　図２　生産関数の例

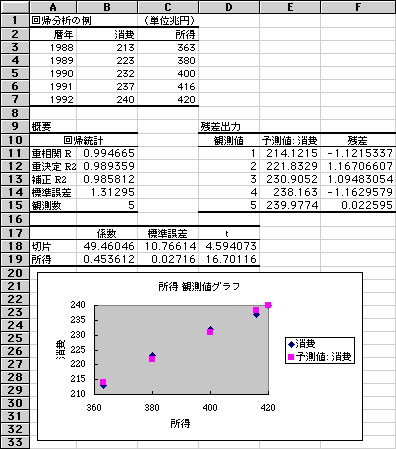
　最後は，統計関係から回帰分析の例を挙げてみましょう．経済学でコンピュータを使うというと計量経済学が連想され，難しいことをしなければいけないような気持ちになってしまいますが，基本的なことは表計算でも十分できるのです．図３はその例です．７行目までが入力するデータで，９行目以下がエクセルが計算した出力結果です．回帰分析は一般に，Y = 定数 + X の形で定式化され，Yの動きをXで説明します．ここでは，消費の動きを所得で説明するという消費関数を推定しています．エクセルには回帰分析用の分析ツールが組み込まれているので，消費のデータをYに，所得のデータをXに指定すれば，図３のような結果をあっという間に打ち出してくれます．ただ，これでは回帰分析の意味を理解したことにはなりません．最初は面倒でも，統計書の回帰分析の計算の手順に従って，回帰係数や切片，決定係数，ｔ値などを自分で式を入力して計算しましょう．回帰分析の意味を理解した後は簡便なエクセルの分析ツールをどんどん利用すればよいのです．

　　　　　　　図３　回帰分析の例


　表計算はその他にも，経済モデルの作成やシミュレーションの分析など様々に応用することができます．
　表計算の経済学への応用を前提にして書かれた文献としては次のようなものがありますので参照して下さい．大藪・安井・藤井・大野『経済学1-2-3：Lotus 1-2-3を使った経済学入門』（日本評論社，1992年），廣松・田中・常磐・木暮『ロータス1-2-3 による統計入門』（朝倉書店，1988年），サイモン・ベニンガ『証券アナリストのための数値計算法』（東洋経済新報社，1991年），拙著『マッキントッシュで経済学』（日本評論社，1994年）．

一歩上を目指して

　表計算の様々な機能を使いこなせれば，それだけでもかなり立派なものですが，表計算の基本をマスターしたなら是非その上を目指して精進されることを希望します．その上とは経済の専門家（大学や企業の研究者）が使用している経済分析用のソフトです．初級と上級の違いは何かと言えば，分析道具がより高度化するということです．初級者向けの分析道具はとりつき易いがそれで高度な分析を試みようとすると大変骨が折れます．他方，上級者向けの分析道具はマスターするにはかなりの努力が要求されますが，一度自家薬籠中のものとしてしまえば後は鬼に金棒です．そのような上級者向けのソフトウェアとして推薦したいのが，MathematicaとRATSです．前者は数式処理ソフトと呼ばれる範疇に入りソフトであり，後者は計量経済分析の専門家が愛用する回帰分析・時系列分析用の統計ソフトです．RATSと同様なソフトにTSPがあり，これもよく使われています．表計算にしても統計ソフトにしても扱えるのは数値だけですが，数式処理ソフトというのは数値に加えて，式そのものを計算してくれるのです．従って，例えば微積分を式のまま解くというようなことができるのです．また数式に基づいた作図能力にも秀でたものがあります．これらの上級者向けソフトは独自のプログラミング機能を備えているので，利用者の目的に沿ったプログラムを組むことができるのです．雰囲気を理解してもらうために，MathematicaとRATSの簡単な例を挙げておきましょう．Mathematicaの例は，マクロ経済学で必ず登場する所得の決定をプログラムしたものです．モデル式を定義し，各変数について解くことを指示すると，連立方程式を記号のまま解いてくれます．外生変数に数値を与えると，数値解も求めることができます．RATSの例は，所得と資産で消費の動きを説明する消費関数を推定するプログラムです．なお，このRATSのプログラムを実行するにはC2.datという名前のデータファイルを事前に作成しておかなくてはなりません．
　表計算を始めとして基礎的なソフトウェアをマスターし，なおかつ専門ソフトをかじりだしたら，パソコンが一層楽しくなり，経済学そのものの理解が深まることは間違いありません．

　　　　Mathematica の例
(* Determination of Income *)
model = {
　　　　y == con + inv + gov,
　　　　con == con0 + mpc yd,
　　　　inv == inv0,
　　　　gov == gov0,
　　　　tax == tax0 + mt y,
　　　　yd == y - tax
　　　　　};
kai = Solve[model,{con, inv, gov, tax, yd, y}]
kai /. {con0 -> 10, inv0 -> 20, gov0 -> 20,
　　　　tax0 -> 10, mpc -> 0.8, mt -> 0.1}

　　　　　　RATSの例
***************************************
*File Name: OLSmlt2.prg
* consumption function: Y = a + b*X1 + c*X2
* open data file C2.dat
* method: OLS
* For Ver.4
***************************************
OPEN DATA C2.dat
CALENDAR 1965 1 1
ALLOCATE 0 1986:1
DATA(ORG=OBS) 1965:1 1986:1 C Y W1
SMPL 1965:1 1986:1
LINREG C
# CONSTANT Y W1
************* end of program *************

登場したソフトウェア一覧

ソフト名	会社名	種類	対応
一太郎	ジャストシステムズ	ワープロ	Mac, Win
マイクロソフトワード	マイクロソフト	ワープロ	Mac, Win
Netscape Navigator	Netscape	Webブラウザ	Mac, Win
Internet Explorer	マイクロソフト	Webブラウザ	Mac, Win
マイクロソフトエクセル	マイクロソフト	表計算	Mac, Win
ロータス1-2-3	ロータス	表計算	Mac, Win
イラストレーター	アドビシステムズ	ドローイング	Mac, Win
ファイルメーカーPro	クラリス	データベース	Mac, Win
パワーポイント	マイクロソフト	プレゼンテーション	Mac, Win
クラリスワークス	クラリス	統合型	Mac, Win
Mathematica	Wolfram Research	数式処理	Mac, Win
RATS	Estima	計量経済分析	Mac, Win
TSP	TSP International	計量経済分析	Mac, Win