IS-LMモデルでは労働市場は含まれていませんでした.財市場と貨幣市場が均衡していても,労働市場が均衡していなければ,失業が発生している可能性があります.労働市場を分析に加えます.
【2009年12月11日更新】
労働の需要[top]
労働の限界生産力説
マクロ生産関数 Y = F(N) (1)
ここで,N は労働投入を表します.
利潤πは生産物の価値から労働投入の費用を差し引いた値になるので,次のようにかくことができます.
利潤 π = P F(N) - W N (2)
ここで,W は賃金率です.
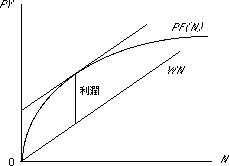
利潤最大化の図解

利潤は生産関数上の点から賃金コスト線の高さを差し引いた垂線の長さで測られます.この垂線の長さが最大となるときが利潤最大です.利潤が最大となるのは賃金コスト線の傾きと生産関数の接線の傾きの大きさが等しい生産関数上の点になります.
生産関数の接線の傾きを労働の限界生産力です.
限界生産力:労働1単位の増加が生産量をどれだけ増加させるかを表します.
利潤を極大化させる条件は,次のようになります.
労働の限界生産力の価値=賃金率
実質賃金と労働の限界生産力が等しくなる点で労働量を雇用すれば利潤が最大となることを意味します.このことをケインズは古典派経済学の基本命題の一つとして挙げ「古典派の第1公準」と命名しました.
古典派の第1公準:
「実質賃金は労働の限界生産力に等しい」
労働需要関数の導出
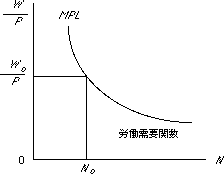
名目賃金率(W)が低下すれば(賃金線の傾き),それに応じて利潤最大化を満たす労働の限界生産力の価値(生産関数の接線の傾き)も低下するので,雇用量(N)も増加(上図を参照).逆の場合は雇用量は減少.従って,縦軸に実質賃金を,横軸に雇用量をとると,各実質賃金に対応して,実質賃金と労働の限界生産力を等しくさせる雇用量の関係を示す労働需要関数は右下がりに描かれます(Pは企業にとっては所与です).
利潤最大化を満たすように雇用される労働の需要は実質賃金が上昇すれば減少します.
労働需要関数
労働の供給[top]
労働者は自分の時間のうちどれだけを労働として供給するか,どれだけを労働以外のレジャーの時間として使用するかを決めます.
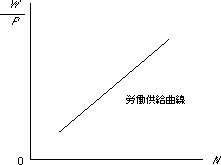
労働供給にとって重要な要素は実質賃金です.実質賃金が上昇すれば,労働者にとって労働時間の供給を増加させる誘因(インセンティブ)が増します.
労働供給関数
賃金上昇の相反する二つの効果
実質賃金が上昇すれば,レジャーに割り当てる時間を減らして,労働に割り当てる時間を以前より多くすることが考えられます(賃金上昇の代替効果).
実質賃金が上昇して所得水準がある程度上昇すると,労働時間をへらしてレジャー等に多くの時間を裂く傾向がでてきます.このことは,労働市場での労働供給量の減少をもたらします(賃金上昇の所得効果).
代替効果>所得効果 → 右上りの通常の労働供給曲線
賃金がかなり高い水準に達した場合は所得効果が上回り労働供給は減少することもありえます(バックウォードベンディング ).
古典派モデル[top]
労働市場の見方については古典派によるとらえ方とケインズ派によるとらえ方の対照的な2とおりの見解があります.
古典派経済学による労働市場のとらえ方の特徴
1.労働需要,労働供給関数はそれぞれ実質賃金の減少,増加関数
2.労働市場の不均衡は実質賃金の速やかな変化によって調整
3.労働需要と労働供給曲線の交点で,労働市場を均衡させる実質賃金と完全雇用が決定
古典派の労働市場と総供給曲線
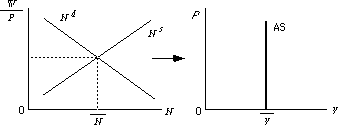
古典派の考え方の特徴:
○労働市場で発生した不均衡は実質賃金のスムースな変化によって早晩解消されるとみなす.
○労働市場で超過供給(失業)が発生したときは実質賃金が低下し,逆に超過需要(人手不足)が発生したときは実質賃金が上昇して完全雇用が常に実現されると考える.
○総供給曲線は完全雇用所得水準で垂直
ケインズ派モデル[top]
ケインジアンによる労働市場のとらえ方
1.名目賃金の下方硬直性
労働需要関数は実質賃金の減少関数.労働供給関数は,ある名目賃金水準では水平部分をもつ.労働の供給は,本来は実質賃金の増加関数となるべきですが(そうでなければ貨幣錯覚),下方硬直性が生じる理由は,一度ある貨幣賃金が成立すると,労働者はその切り下げに反対し,それ以下の貨幣賃金では労働を供給しないと考えられるからです.
2.非自発的失業の存在
労働需要と労働供給曲線の交点で決まる名目賃金とそれに対応する雇用水準は,完全雇用を必ずしも満たさない.
3.労働市場の不均衡は労働市場だけでは解消することができない.
ケインズ派モデルの労働市場と総供給曲線
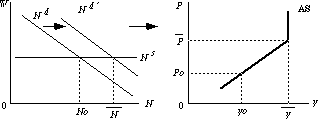
○賃金の下方硬直性を表すために,労働の供給関数はある名目賃金水準で水平
○現在の労働市場の均衡は完全雇用には達しておらず失業が発生.この失業のことを非自発的失業と呼びます.賃金の下方硬直性が存在するときは,失業が発生していても名目賃金は下落しません.
ここで物価が上昇していくとしましょう.実質賃金は下落するので労働需要は増加し,雇用量は増加していきます.左図では労働需要関数の右方へのシフトとなって現われます.右の総供給曲線の図では,物価がPbarまで上昇すると十分実質賃金が低下し,完全雇用が実現.完全雇用が実現した後は,名目賃金は物価水準と同率で上昇していきます.実質賃金は一定.
完全失業者とは[top]
完全失業者とは,調査期間の月末の1週間の間に,仕事がないために1時間以上の仕事をしなかった者のうち,仕事を探しており,かつ仕事があればすぐそれに就くことができる者のこと.詳しくは,以下のメールマガジンコーナーの「完全失業率」を参照してください.
有効求人倍率とは,求職者1人当たりに対する求人件数を示します.
フィリップス曲線[top]
貨幣賃金の上昇率(あるいはインフレ率)と失業率との間のトレードオフ関係をフィリップス曲線(Phillips curve)といいます.英国の経済学者Phillips(1958年)に由来します.フィリップスは長期にわたって賃金(物価)の上昇率と失業率のデータの間には二律背反(トレードオフ)の関係があることを見つけました.物価上昇率が高いときは失業率が低く,逆に失業率が高いときは物価上昇率が低いという関係が安定的に存在しているということです.低インフレ率と低失業率を同時に達成することは不可能という意味で二律背反といわれます.
失業率が高くなれば,労働市場では超過供給が生じていることになり,賃金もしだいに低下していきます.逆に失業率が低下するにつれ労働市場では超過需要圧力が生じるので,賃金は上昇する傾向がでてきます.このような関係が右下がりのフィリップス曲線を生み出す理由です.
その後,1970年代の高インフレ率と不景気(高失業率)の併存(スタグフレーション)を経験することを契機に,ミルトン・フリードマンによるインフレ期待を導入したフィリップス曲線の概念が提案されました.インフレ期待が上昇することにより,フィリップス曲線も右上方へシフトしていくという理論です.
また,フリードマンは,実際のインフレ率が期待インフレ率と一致する長期においては,期待インフレ率を考慮したフィリップス曲線は自然失業率の水準で垂直になると主張しました.長期では,インフレ率と失業率のトレードオフは成立しないということです.
自然失業率(natural rate of unemployment)とは,完全雇用が達成されていてもなお存在している失業率のことです.
メールマガジン[top]
完全失業率については,私のメールマガジンを参照してください.