最近号のメールマガジン
第64回 時系列分析 ARMAとARCH[top]
2003年12月16日更新
2003年11月07日発行
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
国経館 時系列分析 ARMAとARCH メールマガジン No.123
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
みなさん,こんにちは.笹山です.
このメールマガジンは国際経済学科のメールマガジン「国経館」の1つとして,
国際経済学科のすべての学生に配信されています.
今回は,2003年のノーベル経済学賞に関連して時系列分析のお話をします.
マクロ経済学のメールマガジンとしてはNo.64です.
------------------------------------------------------------
【第123号】 時系列分析 ARMAとARCH
------------------------------------------------------------
大学の入門的な経済学の講義で時系列分析(Time Series Analysis)が登場す
ることはほとんどないと思いますが,3・4年生になったらおそらく上級のマ
クロ経済学,計量経済学や金融工学のクラスで学ぶことになると思います.時
系列分析は,今日では経済データを分析する上で,回帰分析と共になくてはな
らない分析ツールになっています.
そのようなわけで,2003年のノーベル経済学賞は,時系列分析の先駆者2
人に与えられました.
『日本経済新聞』10月9日朝刊の記事を紹介しておきましょう.
「スウェーデン王立科学アカデミーは8日,2003年のノーベル経済学賞を
米国人で米ニューヨーク大学のロバート・エングル教授(60)と,英国人で
カリフォルニア大学サンディエゴ校のクライブ・グレンジャー名誉教授(69
)の両氏に授与すると発表した.経済予測などに使われる時系列分析が予測や
分析の精度を高めるのに高い貢献があったと評価した.
時系列分析は時間の経過に伴う株価や金利の動きを数量データにして,変数
の特性を描き出す統計学の一手法.
グレンジャー氏は「共和分」と呼ばれる時系列分析の基礎的な概念を構築し
たことが授賞理由.例えば為替レートと購買力平価がこの関係にあれば長期で
は日米の購買力平価が等しくなる為替レートに収れんしていくことが説明でき
る.
一方,エングル氏は時間の経過に伴いデータの変化の振れ幅が変わる場合に
使う分析手法(ARCH=アーチ)を構築したのが授賞理由.これを応用して
株や金利などを使った金融商品のリスクに対してどの程度のリターンを設定す
ればよいかを計測する手法が開発され,金融取引の活発化などに貢献している.
(抜粋)」
上の記事では「共和分(きょうわぶん)」とか「ARCH」とか,重要なキー
ワードが記されているのですが,多くの方にとってはこの記事の内容は”ちん
ぷんかんぷん”ではないでしょうか.ひょっとしたら記事を書いた記者もよく
わかっていないかもしれません.時系列分析は初めはとっつきにくい分析手法
かもしれません.計量経済学系の分析概念は,理論だけを学ぶよりも,実際デ
ータを集めて分析するとよくわかるようになるものです.時系列分析を学ぶと
き,いきなり「共和分」や「ARCH」からスタートすることはありません.
これらは時系列分析をある程度学んでから登場する概念です.
そこで,今回は時系列分析の入門編として,最も基礎となるARMA(アーマ
と読みます)の概念を紹介します.最後になぜARCHが重要となっているか
を説明します.時系列モデルを説明するときはどうしても式を使わなくてはな
らないので,今回のメールマガジンは少し難しく感じるかもしれません.根気
よく付き合ってください.
■時系列分析とは
時間の経過とともに形成されていくデータのことを時系列データと呼びます.
例えば,株価とか為替レートは毎日市場で値が決まります.それらのデータを
時間の経過にそって並べると一連のデータが得られます.毎日の終値(おわり
ね)を1カ月収集すれば約25個のデータが得られます.1年間集めれば約3
00個のデータになります.このようなデータが時系列データです.
時系列分析(Time Series Analysis)とは,そのようにして集めた時系列デー
タだけを調べることによって,それらのデータの特徴を明らかにしていこうと
する分析手法です.
実は,株価や為替レートなどの金融資産の時系列データは,おもしろいことに
ある規則(法則)に従って動いていることがわかっているのです.その規則を
記述する関係式(あるいは体系)を経済学者は時系列モデルと呼んでいます.
時系列分析のモデルとしては,ARモデル,MAモデル,それにこの両者を総合し
たARMA(アーマ)モデル,ARIMA(アリマ)モデル,それにARCH(アーチ)モ
デルなどがあります.
この中ではARMAが基本です.ARMAとはAutoRegressive Moving
Averageの略称です.日本語にすれば「自己回帰移動平均」です.ARMAは
ARとMAがいっしょになった言葉です.従って順番としてはARモデルから
まず説明し,次にMAモデルにいき,最後に両者を合体させたARMAモデル
へと進んでいくのがわかりやすいでしょう.
■ARモデル
時系列分析では,あるデータの動きの特徴を探るときは,そのデータ自身の持
っている特性をモデルに基づいて詳細に探るというアプローチをとります.い
わばデータのことはデータ自身にきけという立場です.ARとは
Autoregressive の略で自己回帰となります.自己回帰とは,自らの動きを自
らの過去の値で説明することを意味します.
時系列データの集合を{yt}とします.例えば,yが為替レートの毎日の終値
とすればtを1カ月とすればこの集合の中にはデータが25個入っていること
になります.以下ではy は為替レートとして話を進めます.
{yt}について,ARモデルは一般的には次のようにかけます.
y(t) = μ' + φ1 y(t-1) + φ2 y(t-2) +...+ φt-p y(t-p) + u(t) (1)
今期(t期)の為替レートの動きは1期前,2期前,...p期前までの為替
レートと今期の攪乱項u(t)によって説明されることになります.
μ'やφはパラメーター(定数)で,u(t)はホワイトノイズ(white noise白色
雑音)の性質を満たす撹乱項(あるいは誤差項)です.
ホワイトノイズというのは,以下の3点を満たす時系列のことをいいます.
(1)平均がゼロ:
(2)分散が一定:
(3)自己共分散がゼロ:
分散はデータのばらつき度を測る尺度です.自己共分散とはみずからのデータ
の例えば1期前のデータと2期前のデータの間に相関関係がないことを意味し
ます.ここでいう攪乱項(ホワイトノイズ)というのは,確率的に決まる変数
であり,どのような値がでてくるかは事前にはわかりません.ただし,まった
くでたらめというのではなく,この攪乱項はある一定の幅内で不規則(ランダ
ム)に変動し,全体を通して平均すればゼロとなるような変数です.光の性質
を調べると,その中の白色が持っている性質に似ているのでホワイトノイズと
いう名前がついています.
ホワイトノイズというのは言い換えれば自己相関の全くない確率変数です.
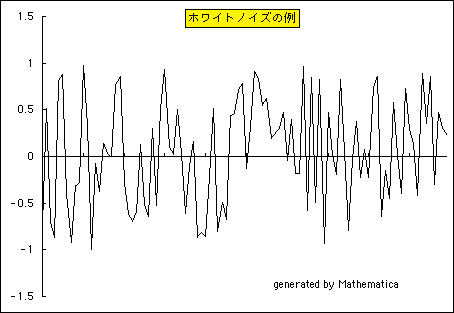
ホワイトノイズのデータはどのような形をしているのかを示しておきましょう.
これはあくまでも1つの例です.
ホワイトノイズの例:

この確率変数である攪乱項(ホワイトノイズ)のグラフの形状を頭に入れてお
いください.トレンド(傾向)を持っているデータとか,変動の振幅がしだい
に大きく(あるいは小さく)なっていくようなデータ,サイン・コサインカー
ブに似た動きを示すデータ等はホワイトノイズではありません.
AR(1)の例
ARモデルの中でも最も基本的な,1次の自己回帰モデルAR(1)(First-
Order Autoregressive Model)は次のようにかけます.
y(t) = μ' + φ y(t-1) + u(t) (2)
ここでφを自己回帰係数と呼びます.φの絶対値は1以下であることが必要で
す.μ'は定数項で,u(t)はホワイトノイズを満たす撹乱項です.
AR(1)モデルでは,自己回帰係数φの値によってどのような時系列になるかが
決まってきます.φが1の場合がランダムウォークという特別なケースになり
ます(メールマガジン:「ランダムウォーク」の項を参照してください).
ホワイトノイズのデータは,表計算ソフトエクセルでは次のような関数を使い
ます.
=RAND()*(-1-1)+1
ホワイトノイズのデータが用意できればAR(1)モデルは簡単に作り出すこ
とができます.(2)式でμ'はゼロとし,yの初期値に1を与えてやれば,
(2)式に基づいてyのデータを順繰りに作り出すことができます.
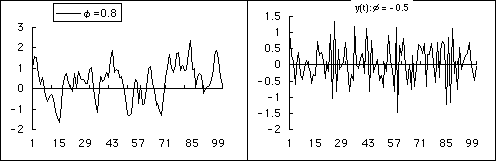
φの値が0.8の場合と,-0.5の場合の例を計算してみましょう.φの値の正負
に応じて形状が異なることに注目しましょう.その他,φの値を様々に変えた
とき時系列yはどのような形状を示すかも観察しましょう.
AR(1)の例: y(t) = 0.8 y(t-1) + u(t) y(t) = - 0.5 y(t-1)
+ u(t)
■MAモデル
時系列モデルの2つ目としてMAモデル(Moving Average model)があります.
一般的には次のように表されます.
y(t) = μ + u(t) - θ1 u(t-1) - θ2 u(t-2) - ... -θq u(t-q) (3)
ここで,μやθはパラメーター(定数),u(t)はホワイトノイズを満たす撹乱
項です.MAモデルはARモデルとは違って,y(t)を今期から過去にさかのぼった
撹乱項についての移動加重和として表わされます.1やθはウェイトとみなせ
ます.ただし,ウェイトの合計は1になる必要はありません.θの絶対値は1
以下であることが必要です.
(注意)経済学では,もう1つの「移動平均」(moving average)の概念があ
ります.データの平均を計算するときデータを1つずつずらしながら平均値を
計算する方法です.例えば30日間移動平均とか,90日間移動平均などとい
う名称で登場します.これも移動平均と呼んでいます.時系列分析のMAモデ
ルとはまったく別物ですので混同しないでください.
(3)はq 期前までさかのぼっているのでq次のMAモデルと呼ばれ,MA(q)と
かきます.
MAモデルのうち最も基本的な1次の移動平均モデルMA(1)(First-Order
Moving Average Model)は次のように表されます.
y(t) = μ + u(t) - θ1 u(t-1) (4)
MAモデルでは定数項μはデータの平均値と一致する性質があります.MAモ
デルも,ホワイトノイズのデータがそろっていれば(3)式に基づいてy(t)の
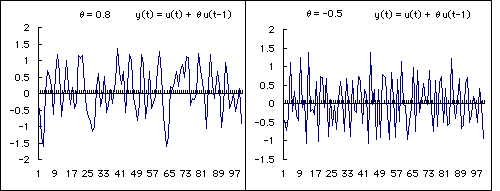
系列を作り出すことができます.μ=0として,θの値をさまざまに変えてシ
ミュレーションしてみましょう.
MA(1)の例: y(t) = u(t) + 0.8 u(t-1) y(t) = u(t) - 0.5 u(t-1)
■ARMAモデル
ARモデルとMAモデルを合わせたのがARMA(AutoRegressive Moving
Average)モデルです.
時系列データ{yt}について,ARMA(アーマ)モデルは次のようにかけ
ます.
y(t) = μ' + φ1 y(t-1) + φ2 y(t-2) +...+ φt-p y(t-p)
+ u(t) - θ1 u(t-1) - θ2 u(t-2) - ... -θq u(t-q) (5)
ARの次数がp,MAの次数がqなのでARMA(p, q)とかきます.代表的なARMA(1, 1)
は次のようになります.
y(t) = μ' + φ1 y(t-1) + u(t) - θ1 u(t-1) (6)
ARMAの場合もホワイトノイズu(t)のデータがあれば,φ1とθ1の値を設定
し,yの初期値を与えてやれば,y(t)の時系列データが順繰りに決まります.
y(t) = + 0.9 y(t-1) + u(t) + 0.8 u(t-1)
y(t) = - 0.5 y(t-1) + u(t) - 0.5 u(t-1)
■ARCHモデル
ARCH(アーチ,AutoRegressive Conditional Heteroscedastic)モデル.
日本語では,分散不均一の自己回帰過程と呼んでいます.
まず,なぜARCHモデルが重要なのかを説明しておきましょう.これまで説
明してきたARMAモデルでは,時系列データの残差はホワイトノイズという
前提で議論されていたのですが,為替レートや株価などの金融資産の時系列デ
ータを詳しく調べてみると,実は残差はホワイトノイズの性質を満たしていな
いことがわかったのです.金融資産時系列データの残差の分散は一様ではなく
ばらつきに特徴があることがわかったのです.どのような特徴かというと,例
えば為替レートの場合であれば,ある期間大きく円高方向に変化した場合はそ
の後で逆に円安方向に大きく変化する期間が続くという性質です.このような
性質を「分散の不均一性(heteroscedasticity)」と呼んでいます.
このような分散の不均一性を組み込んだ時系列モデルがARCHであり,20
03年ノーベル経済学賞を受賞したエングル(R.F. Engle)が1982年に発
表したモデルです.
ARCHモデルでは,今期の分散が過去の分散に依存することをモデルに組み
込みます.これが,分散不均一の自己回帰過程(ARCH)の意味です.
AR(1)モデルの1つであるランダムウォークの誤差項を入れ換えてARCHを説明
します.これが一番わかりやすいと思います.
ランダムウォーク: y(t) = y(t-1) + u(t) (7)
u(t)はホワイトノイズ
ARCHモデルでは,上の攪乱項u(t)はホワイトノイズではなく,以下のu(t)
で置き換えます.
y(t) = y(t-1) + u(t) (8)
u(t) = v(t) SQRT(a0 + a1 u(t-1)^2) (9)
ここで,v(t)が平均0,分散1のホワイトノイズになります.a0 > 0, 0 <
a1 < 1 です.SQRTは平方根を意味します.
上のモデルでは,分散が1期前の分散に依存するのでARCH(1)といいます.
残差の2乗は1期前の残差の2乗に依存します.a0=1 and a1=0 のとき,
ARCHはランダムウォークと同じになります.
Engle, R.F.(1982),"Autoregressive Conditional Heteroscedasticity
with
Estimates of the Variances of United Kingdom Inflation,"
Econometrica,
Vol.50, No.4, pp.987-1007.
■GARCHモデル
EngleのARCHモデルを拡張したのが彼の弟子BollerslevによるGARCH
(ガーチ,Gereralized ereralized AutoRegressive Conditional
Heteroscedastic)モデルです.ARCHモデルの条件付き分散が過去の分散だけ
でなく過去の残差の2乗にも依存するという関係を組み込みました.ARCH
からGARCHへの拡張は,ちょうどARをARMAに拡張したのと対応して
います.
GARCHモデルの代表的なGARCH(1,1)を紹介しておきましょう.
y(t) = y(t-1) + u(t) (10)
u(t) = v(t) SQRT(h(t)) (11)
h(t) = a0 + a1 u(t-1)^2 + b1 h(t-1) (12)
ここで,a0 > 0, a1 + b1 < 1.u(t)はホワイトノイズではなく,v(t)がホ
ワイトノイズになります.
金融資産時系列データの分散の不均一性をとらえるモデルとしては,ARCH
よりもGARCHの方がすぐれていることが今日ではわかっています.ノーベ
ル賞はオリジナリティのある研究に授けられるので,ARCHの概念を最初に
提案したエングルが受賞したわけです.
■関連文献の紹介
Bollerslev, T.(1986),"Generalized Autoregressive Conditional
Heteroskedasticity," Journal of Econometrics, Vol.31,
No.3, pp.307-
327.
GARCHに関する基本文献です.
市川博也「入門マクロ経済の時系列分析」『経済セミナー』2003年4月号から
学部学生向けにわかりやすく書かれています.
■関連サイトの紹介
2003年度ノーベル経済学賞紹介のオフィシャルサイトが何といっても充実
しています.2003年12月8日に受賞記念講演が行われます.これはイン
ターネットで中継されます.
2003年ノーベル経済学賞:
http://www.nobel.se/economics/laureates/2003/index.html
受賞発表ページ
★http://www.nobel.se/economics/laureates/2003/ecoadv.pdf
本格的な業績紹介
http://www.nobel.se/economics/laureates/2003/public.html
業績紹介の要約版
Engle教授のサイト(ニューヨーク大学ビジネススクール):
http://pages.stern.nyu.edu/~rengle/
Granger教授のサイト(カリフォルニア大学サンディエゴ校):
http://econ.ucsd.edu/~cgranger/
■まとめ------------
・株価や為替レートなどの金融資産価格の統計的な特徴を調べることを時系列
分析と呼ぶ.
・代表的な時系列モデルには,AR,MA,ARMA,ARCHなどがある.
・ARMAモデルでは残差はホワイトノイズを前提としているが,実際の金融資産
の残差はホワイトノイズにはなっていない.
・金融資産価格時系列の残差の分散には不均一性が認められる.
・分散の不均一性をモデルに取り込んだのがエングル教授によるARCHモデ
ルである.
・現在ではARCHの拡張版であるGARCHモデルの方が分散の不均一性を
よくとらえることができる.
-------------------------------------
【課題】
2003年12月8日にはノーベル経済学賞の受賞講演がインターネットで世
界中に中継されます.エングルとグレンジャー両教授の講演を聴いてください.
エングル教授の講演(Prize Lecture, 41分間):
http://www.nobel.se/economics/laureates/2003/engle-lecture.html
グレンジャー教授の講演(Prize Lecture, 33分間):
http://www.nobel.se/economics/laureates/2003/granger-lecture.html
(注意)後日サイトにアクセスした場合,サイトの構成に違いがでてきたり,
URLが変更になっている場合がありますので,了解してください.
(アクセス日)2003年11月7日
------------------------------------------------------------
【Q & A】ARMAモデルは何と何から成っている?
→ AR(自己回帰モデル)とMA(移動平均モデル)
【今回のサイト】 2003年ノーベル経済学賞:
http://www.nobel.se/economics/laureates/2003/index.html
【評価】★★★
私の評価の基準:最高が★★★,次が★★,最後が★です.
★1つは普通という評価です.
データが十分提供されているかどうかが評価のポイントです.
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
【発行】 熊本学園大学 経済学部 国際経済学科
【著者】 笹山 茂
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
Copyright 2003