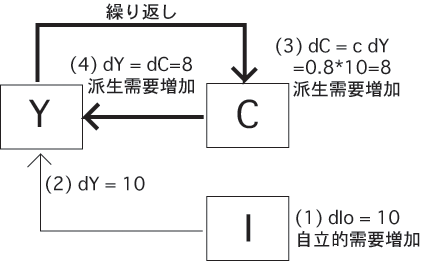
自立的需要の増加(上の図ではdIo=10, c =0.8 )
→それに見合った生産の増加→所得の増加(dIo = dY)
2015年1月5日更新
政府が公共投資を増加したり,あるいは企業が投資を
増加させることによって,国民所得は増加することが
予想されますが,それはどの程度増加するのであろうか.
あるいは,そのメカニズムはどうなっているのかを探
るのが乗数分析のねらいです.
経済的な波及メカニズム(乗数の考え方)
(例)パソコンの需要増大が経済全体の景気に与える効果
パソコンが50億円余分に売れたとします
→メーカーは50億円余分に生産し販売します
→売上増加の50億円は従業員の賃金の増加や利潤の
増加として50億円の所得増加をもたらします.
(ここまでが自立的需要増加)
経済への波及効果は上だけに留まりません.
所得の増加したパソコンメーカーの従業員は,所得増加
の一部をその他の消費財(洋服,旅行,外食など)への
支出に向けます.
それらを生産している企業の生産も増大し,そこで働
いている従業員の所得も増加します.
従ってこれらの従業員も様々な商品を購入するので,
さらにその他の企業の生産も増大します.
このような循環が際限なく繰り返されるのです.
(この部分を派生需要の増加といいます)
投資乗数[top]
単純な経済モデル
財市場の均衡式 Y= C + I (1)
消費関数 C = Co + c Y (2)
投資支出 I = Io (3)
モデルの図式

自立的需要の増加(上の図ではdIo=10, c =0.8 )
→それに見合った生産の増加→所得の増加(dIo = dY)
派生需要の増加:
上で生じた所得増加によってもたらされる需要の増加
=限界消費性向×所得増加
派生需要は無限に近く繰り返されます.
最終的な需要(所得)の増加
=自立的需要増加+派生需要の合計
=10 +(0.8*10 +0.8^2*10 +0.8^3*10 + .. +
+ 0.8^n*10+..)
= 10( 1 + 0.8 + 0.8^2 + 0.8^3 + ・・+ 0.8^n +
+ ...)
( )内は初項1,公比0.8の無限等比数列
= 10 ( 1 / (1 - 0.8) ) (公式 初項/(1 - 公比)から)
= 10 ×5 = 50
一般的に記号で書くと,
=dIo +(cdIo +c^2dIo +c^3dIo + .. +
+c^ndIo+..)
=dIo (1+c+c^2+c^3+...+c^n+...)
![]()
上で( )内は初項1,公比cの無限等比数列
【公式】無限等比級数の和=初項/(1ー公比)
(注)無限等比数列の和の公式は,
以下の「高校数学の復習:等比数列」の項目を参照してください.
(重要)
自立的支出増加
所得増加= ---------------------
1−限界消費性向
限界消費性向=消費の増加分/所得の増加分
0<限界消費性向<1
dIo =10,c=0.8ならば,このときの最終的な需要
増加額は
dY = 10/(1 - 0.8) = 50
10億円の初期需要の増加によって,最終的には
その5倍の50億円の所得増加を経済全体にもたら
します.
この倍数のことを乗数と呼びます.この例では
乗数は5となります.
式による求め方
乗数は,均衡所得を求めることから得られることを
示しましょう.
(2)と(3)を(1)に代入し,
Yについて解くと均衡所得が得られます.
Y = Co + cY + Io
Y = cY + Co + Io
(1-c)Y = Co + Io
![]() (4)
(4)
ここで,上のモデルの(3)式の投資がdIoだけ増加
したとしましょう.すると,
財市場の均衡式 Y= C + I (1)
消費関数 C = Co + c Y (2)
投資支出 I = Io + dIo (3')
均衡所得の求め方は,(2)と(3’)を(1)に
代入してYについて解きます,
![]() (5)
(5)
(5)-(4)が所得の増加を表します.
所得の増分をdYとかくと,
![]() (6)
(6)
実は,(4)式の係数部分,
1/(1-c) が乗数の値に等しくなっているのです.
(別解)
(6)式を得るにはもっと簡単な方法があります.
最初の均衡所得の式(4)を元に考えます.
(4)式で変化する部分だけを取り出せばいいのです.
変化した部分の記号にはdという記号を頭につけます.
例えば,Yが変化した部分はdYと書きます.
dYでひとまとまりの記号です.
投資 Io だけが増加した場合,それによって影響を
受けるのは左辺のYです.
右辺の係数 1/(1-c) はそのまま付きます.従って,
変化した記号dをつけて書けば,
(6)式のようになるのです.
●(重要)
限界消費性向が大きければ大きいほど,乗数は大きい.
所得の増加のうち,消費に振り向けられる割合(限界消費性向)
が大きければ大きい程,追加的に支出される消費需要が
大きくなるので,派生需要の合計もその分大きくなるからです.
---------------------------------------------------
政府支出乗数[top]
政府を追加した経済モデル
財市場の均衡式 Y= C + I + G(7)
消費関数 C = Co + c Yd (8)
投資支出 I = Io (9)
政府支出 G = Go (10)
税収 T = To (11)
可処分所得 Yd = Y - T (12)
モデルの図解
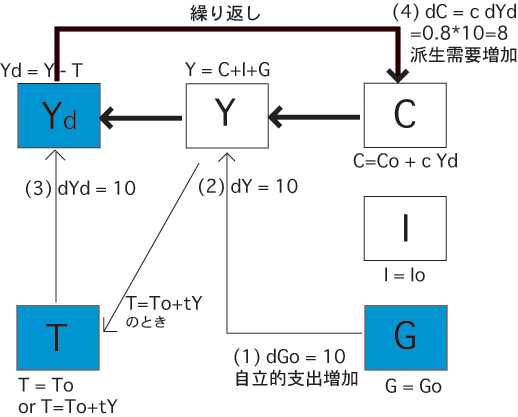
上のモデルの場合,
均衡所得は((8)から(12)を(7)に
代入してYについて解きます),
Y = Co + cYd + Io + Go
Y = Co + c(Y - To) + Io + Go
Y - cY = Co - cTo + Io + Go
(1-c)Y = (Co - cTo + Io + Go)
![]() (13)
(13)
政府支出がdGoだけ増加すると,所得の増加は上式から,
![]() (14)
(14)
政府支出乗数は1/(1-c)です.
租税乗数[top]
減税の乗数効果を分析してみましょう.
モデルは政府支出乗数と同じモデルを使います.
従って,均衡所得は(13)式です.
減税の場合はToの部分だけが変化します(-c dTo).
従って,
![]() (15)
(15)
租税乗数はc/(1-c)となります.政府支出乗数に
比べると小さくなります.なぜでしょうか?
政府支出の場合は,最初にdGoの増加の効果が現れます.
ところが減税の場合は,まず可処分所得の増加と
なって現れ,可処分所得のうち限界消費性向分だけ
の消費増加が最初の所得増加となって現れます.
第1回目の所得増加から差がついているのです
(モデルの図解参照).
○ビルト・イン・スタビライザー(built-in stabilizer)
景気がよいときは税収が増えて,これが景気の過熱を
冷まし,
他方,景気が悪化したときは税収が低下することで
(減税の効果)景気回復を助けることになります.
このように税収には自動的に景気を安定化させる機能
をもっています.
これを税収がもつビルト・イン・スタビライザーと
いいます.
均衡予算乗数[top]
政府が均衡予算を維持するように財政支出を増加させ
たときの乗数効果はどうなるか,というのが問題意識.
ここで,均衡予算とは政府の支出はすべて税収に
よって賄う,すなわち赤字国債は発行しないことを
意味します.
従って,例えば1兆円の政府支出を実行するには
1兆円の増税によってまかなわれます.
1兆円の政府支出は1兆円の増税によって完全に
相殺されて,乗数効果はゼロになるのでしょうか.
実は「均衡予算乗数は1である」というのが解答です.
証明は,政府支出乗数と租税乗数を総合すればいいのです.
このとき均衡予算なのでdGo=dToを前提とします.
また,今回は減税ではなく増税なので租税乗数の符号は
マイナスになることにも注意しましょう.
![]() (16)
(16)
日経新聞のコラムの筆者は,均衡予算乗数のことを
大学で勉強しなかったわけですね(練習問題集の【問題9】を参照.
以下の「新聞記事の誤りを見つけよう」も参照).
均衡予算であっても政府支出の増加分だけはGDPの増加
となって現れるのです.
外国貿易乗数[top]
開放経済モデル
財市場の均衡式 Y = C + I + G + EX - IM
(17)
消費関数 C = Co + c Yd (18)
投資関数 I = Io (19)
政府支出 G = Go (20)
輸出 EX = EXo (21)
輸入関数 IM = IMo + m Y (22)
可処分所得 Yd = Y - T (23)
税収 T = To (24)
クイズその5
上のモデルから,均衡所得を計算し,それを使って
輸出が増加したときの乗数を求めなさい.
ケータイマクロ練習問題[top]
財市場のみを考慮した封鎖経済マクロモデルを考えます
(海外部門は省略した政府支出乗数モデル).
このとき増税と政府支出増加を共に2兆円ずつ同時に
実施した場合,GDPへ与える効果はどうなるでしょうか.
ただし,限界消費性向は0.8,租税収入は定額税とします.
1 GDPは最終的に1兆円増加する
2 GDPは最終的に2兆円増加する
3 GDPは変化しない
新聞記事の誤りを見つけよう[top]
(その2)
新聞の記事やコラムにも,経済理論からすると
”とんちんかんな”内容が掲載されることがときどき
あります.
そのような例を,上記の「総合経済対策」関連から
見つけることができました.
日経新聞1998年5月2日朝刊3面
「消費一部に下げ止まり感.消費性向3月3.3
ポイント上昇.3月家計調査」
要点だけを部分的に引用します.
「総務庁が1日発表した3月の家計調査によると,
全世帯の消費支出(消費税込み)は平均で36万898円で,
物価変動の影響を除いた実質で前年同月比5.7%減少した.
... 前月比(季節調整値)では3.8%増と2カ月ぶりに増加
した.サラリーマン世帯の可処分所得に占める消費支出
の割合を示す平均消費性向(季節調整値)も前月より
3.3ポイント高い71.7%と7カ月ぶりに上昇しており,
特別減税が個人消費悪化に一応の歯止めをかけた
ことを示した.」
上の新聞記事(特に太字の部分に注目)のどこが
おかしいかわかりますか?
ポイントは「平均消費性向」と「限界消費性向」
の区別です.平均消費性向が上昇したことで,
はたして個人消費の悪化に歯止めがかかったと主張
できるでしょうか? 答えはNOです.
ケインズ型の消費関数の場合,所得が増加するに
つれて平均消費性向は低下しますから,平均消費
性向が増加したというのは,単に所得が低下した
だけかもしれないのです.限界消費性向が増加し
たというのであれば,所得の増加のうち消費へ振
り向ける部分が増加するので,消費活動が活発に
なったといえるでしょう.限界消費性向が増加す
れば,乗数も増加します.
もう1つ,代表的な消費関数の考え方である「恒
常所得仮説」に基づいて考えてみましょう.この
場合も,所得の増加が恒常的とみなされて短期の
消費関数が上方へシフトする前の段階では,平均
消費性向は低下します.
平均消費性向の増加が消費の増加と解釈されるの
は,消費関数全体が上方にシフトする場合です.
ただし,消費関数が上方にシフトするには恒常所
得の増加が明確に認識されなくてはなりません.
今日の状況はそのような環境にはありません.
従って,どちらの見方でも,平均消費性向の上昇
と消費の悪化の歯止めを結びつけるのは無理です.
このように,新聞記事には経済理論からみると誤
った内容が書かれることがときどきあります.
新聞記者の中にも経済学を十分学んでいない者も
いるわけです.
(その3)
以下の文章は1995年7月27日付『日本経済新聞』
朝刊の「大機小機」欄に掲載されたコラムの前半
部分です.マクロ経済学を学んだ人がこの文章を
読めば,コラムの筆者はマクロ経済学の基礎を理
解していないことがわかります.
「景気対策をめぐる議論で理解しがたいことは,
政府の支出規模ぱかりが話題になることだ.しかし,
景気刺激効果があるのは支出規模ではなくて,政府
支出と政府収入の差である財政赤字額である.
政府が税金でお金を集めて,それを公共事業に回
してもネットの景気刺激効果はほとんどない.政府
がA氏のポケットからお金を集めて建設会社に仕事
を回せば,建設会社の景気は良くなるが,A氏の景
気は悪くなるので,日本全体としては景気は良くな
らないからだ.他のことでは教養ある人々がなぜ
こんな簡単な理屈を理解されないのかまったく不思
議である.」
上の下線部分に特に注目してください.これは
「均衡予算乗数はゼロである」と主張していること
になります.「均衡予算乗数」の項で説明したとおり,
同乗数は1です.税金でお金を集めて公共事業を
行っても支出した分はGDPの増加となってあら
われるのです.このコラムを書いた方は,均衡予算
乗数を学んでいなかったのですね.
インターネットで探そう・緊急経済対策[top]
政府は景気回復をはかるために,1998年以降立て
続けに緊急経済対策を実施しています.
1998年4月24日には,総額16兆円にものぼる
「総合経済対策」を,続けて1998年11月16日には
総額23兆円の「緊急経済対策」を発表しました.
政府の財政政策は,まさに乗数効果が発揮される
ことを前提に行われています.
それぞれの対策の内容は首相官邸や内閣府(旧経済企画庁)のHPで読むことができます.
・1998年4月24日 「総合経済対策」16兆円(橋本内閣)
・1998年11月16日 「緊急経済対策」23兆9000億円(小渕内閣)
・1999年11月11日 「経済新生対策」18兆円を政府決定
財政支出9兆円前後(小渕内閣)
・2000年10月19日 政府,経済対策「日本新生のための新発展政策」(pdf)発表
総額11兆円,国費投入分は3.9兆円兆(森内閣)
・2001年4月6日 政府・与党「緊急経済対策」を発表(森内閣)
「緊急経済対策のポイント」
不良債権2年で処理.「銀行保有株式取得機構」の設立
・2002年2月27日 早急に取り組むべきデフレ対応策(pdfファイル)
首相官邸 http://www.kantei.go.jp/
内閣府 http://www.cao.go.jp/
内閣府 経済見通し,経済対策:
http://www5.cao.go.jp/keizai1/mitoshi-taisaku.html
最近の経済対策の発表文はここに整理されてあります.
以上のような財政政策を実施したにもかかわらず,
1990年代の日本経済のことを「失われた10年」と
呼ばれています.この間,ほとんど経済は成長しな
かったのです.なぜ,財政政策は十分効果を発揮し
なかったのでしょうか?考えてみてください.
実際の乗数はいくら(ネット情報)[top]
2003.11.04(火) 内閣府,公共投資の乗数効果が縮小,1.1倍.減税の乗数効果は0.48倍
http://www.esri.go.jp/jp/archive/e_dis/e_dis080/e_dis075.html
(要約)
http://www.esri.go.jp/jp/archive/e_dis/e_dis080/e_dis075a.pdf
(全文98ページ)
内閣府,経済社会総合研究所による分析結果です.
新聞関連記事[top]
地域振興券は98年11月の「緊急経済対策」23兆円
の一部として実施された政策です.総額は7500億円です.
15歳以下の子供のある家庭に1人2万円,65歳以上
で所得のない人に同じく1人2万円の商品券が支給
されました.政府は,この最初の消費増加(自立的
支出増)で派生需要が増加することをもくろんだの
でしたが,大方の予想通り,期待した効果は得られ
ませんでした.
講義ノートのイントロダクション,
「1999年4月の話題」も読んでください.
地域振興券関連の記事をいくつか紹介しておきましょう.
・2000.09.19 地域振興券,消費喚起効果は軽微.75%が支出変わらず(日経流通新聞)
・2000.01.07 地域振興券,6割強,貯蓄に流れる(日本経済新聞)
・1999.08.06 経済企画庁,地域振興券,個人消費0.1%押し上げ.交付額(6193億円)の3割(2025億円)が新規の消費に回った
・1999.05.01 地域振興券の使途,大半が食料・日用品(日本経済新聞)
以下のコラムは,最近乗数の大きさが低下している
ことを具体例を挙げながら説明しています.
●佐和隆光「車とパソコンの違いとは.経済波及効果
に大きな差」(日本経済新聞1998年6月14日 Monday Nikkei)
・日経新聞,2004年7月9日,「猛暑,景気に追い風,GDP0.1 - 0.3%押し上げ」
・第一生命経済研究所,猛暑になればGDPを0.14%押し上げ
http://group.dai-ichi-Life.co.jp/dlri/news/pdf/nr2004_10.pdf
(2004.06.11公表)
(注)これらの日本経済新聞の記事は,日経の有料データベース「日経テレコン21」で検索することができます.
高校数学の復習:等比数列[top]
乗数の計算のところでは,高校数学で学んだ
「等比数列」を使っています.復習をしておきましょう.
次のような数の並びを「等比数列」といいます.
例)2,4,8,16,32,64,128,256,...
最初の項が2で,2番目の項は,最初の項に2を
かけています.
3番目の項は2番目の項に2をかけています.
このように前の項に一定の数を順々にかけている
ことがわかります.
このとき,最初の項を「初項」,毎回かけている一定の
数を「公比」といいます.
上の例では,初項は2,公比は2です.
数値例はたくさん作ることができますが,
記号を使って一般的に書くことをやってみましょう.
数列の初項をa,公比を r とすると,等比数列は
次のようになります.
a, ar, ar*r, ar*r*r, ar*r*r*r, ....
ここで,r*r = r^2(2乗), r*r*r = r^3(3乗),
というように書きます.^は通称”ハット”と読みます.
小さな上付き文字が使えないので,このようにハット
記号を使います.
また,ハット(^)はコンピュータでは「〜乗」の
記号として必ず使うので,この機会にぜひ覚えてください.
すると,上の数列は,次のようになります.
a, ar, ar^2, ar^3, ar^4, ....., ar^n-1, ar^n(1)
(1)の数列では,1番目(a)からn+1番目(ar^n)
まで並べてあります.
(1)で,nの値が無限に続く場合を無限等比数列といいます.
次のようになります.
a, ar, ar^2, ar^3, ar^4, ....., ar^n-1, ar^n, ..(2)
n-> ∞(無限大を表す記号)となり,限りなく続きます.
■無限等比数列の和
次に,(2)で表される無限等比数列の和(合計)
を計算するにはどうしたらよいかを考えます.
無限等比数列の和をAで表すことにします.
A=a + ar + ar^2 + ar^3 + ar^4 +...+ ar^n-1 + ar^n + ...(3)
(3)式の左辺と右辺に r をかけます.
rA=ar + ar^2 + ar^3 + ar^4 +....+ ar^n + ar^(n+1) + ......(4)
(3)の両辺から(4)の両辺を差し引きます.すると,
次のように簡単になってしまうのです.
A - rA = a (5)
(3)と(4)の右辺は無限大に続くので,
(3)と(4)の違いは,(3)の方が最初の項aが
多いだけなのでこのように消えてしまうのです.
(5)より,
a
A = --------- (6)
1 - r
言葉でかけば,
(重要)以下の公式は必ず覚えよう.
初項
無限等比数列の和 = ------------------
1 − 公比
上が「無限等比数列の和の公式」です.
公比が1のケースは除きます.
(注1)無限等比数列にはある一定の値に収束
する場合と収束しない場合がありますが,
われわれは収束するケースを対象にします.
私のメールマガジン
「経済数学の基礎(マクロ経済学編)等比数列」も読んでください.
ケータイマクロ問題[top]
無限等比数列
10 + 6 + 3.6 + 2.16 + 1.296 + ...
の和は以下のどれでしょう.
1. 23
2. 25
3. 27
付録:エクセルファイル[top]
乗数分析を表計算ソフト,エクセルを用いて
シミュレートすることができます.
multpl.xls (エクセルファイル)
クリックするとダウンロードすることができます.
付録:等比数列
高校数学の復習,等比数列
tohisuretu.pdf (pdfファイル)