関連するメールマガジン
第73回 経済数学の基礎(マクロ経済学編) 常用対数と自然対数[top]
2004年6月4日発行
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
国経館 経済数学の基礎 常用対数と自然対数 メールマガジン No.138
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
みなさん,こんにちは.マクロ経済学を担当している笹山です.
このメールマガジンは国際経済学科のメールマガジン「国経館」の1つとして,
国際経済学科のすべての学生に配信されています.
今回は,経済学でよく使われる自然対数の話です.
マクロ経済学のメールマガジンとしてはNo.73です.
------------------------------------------------------------
【第138号】 経済数学の基礎 常用対数と自然対数
------------------------------------------------------------
大学の経済学では「自然対数(しぜん・たいすう)natural logarithms」が登
場します.高校の数学の教科書には自然対数の説明はありません.高校で習う
対数は「常用対数(じょうよう・たいすう)base 10 logarithms」です.この
あたりに大学での経済学,あるいは経済数学が難しいと感じる理由の1つがあ
るかもしれません.今回は,自然対数の経済的な意味を明らかにしておきたい
と思います.自然対数は経済成長や銀行に預金をした場合の元利合計の複利計
算などでよく使われており,実は結構身近な存在なのです.
内容の性格上,式が多く登場してきますが,根気よくつきあってください.後
半では数式処理ソフト Mathematica での計算方法も紹介しておきます.
■高校数学では常用対数
まずは高校数学(数学 II)の復習から始めましょう.
(対数の定義)-----------------------
a > 0 かつ a は1でないとするとき,指数関数 y = a^x で,任意の正の実数
Mに対して(M > 0)
a^p = M
となる実数pがただ1つ決まる.このpを
log a M
と表し,これをaを底(てい)とするMの対数という.Mをlog a Mの真数(しん
すう)という.
(常用対数)
10 を底とする対数 log 10 M を常用対数(じょうよう・たいすう.base 10
logarithm)という.
------------------------------------------------------------------
(対数の性質)-----------------------
[1] log a M N = log a M + log a N
[2] log a M/N = log a M - log a N
[3] log a M^r = r log a M
------------------------------------------------------------------
(底の変換公式)-----------------------
a, b, c が正の数で,a とc は1ではないとき,次の等式が成り立つ.
log c b
log a b = -------------
log c a
------------------------------------------------------------------
(例)
log 10 100 = 2 10を底とする100の対数は2 と言います.
10^2 = 100 と同じことになります.
対数の底は10以外でもいいのですが,高校でなぜ10を底とする常用対数を学ん
だのかといえば,われわれは10進法に慣れ親しんでいるということでしょう
か.
以上が,高校の数学の教科書に記載されている主な内容です.
■経済学では自然対数
経済学では常用対数でなく自然対数が使われます.自然対数とは何かをまず理
解しましょう.
(自然対数)-----------------------------
e を底とする対数 log e M を自然対数(しぜん・たいすう base e
logarithm)という.
ここで e とはe = 2.7182818...となる無理数.
log e x = y <=> e^y = x
log e x を簡単に ln x とよく書きます.ln はnatural logarithmを表します.
ln x = y では,xをえるためにはeを何乗(y)したらよいのかを意味しています.
e^(ln x) = x あるいは ln e^x = x
無理数(irrational number)には,皆さんがよく知っているものとしては,π=
3.1416...がありますが,それと似た概念だと思えばいいでしょう.
------------------------------------------------------------------
経済学では,常用対数でなく自然対数なのはなぜ
自然対数の底 e = 2.71828...は,1万円を年利率1(100%)の複利で預金し
たときの元利合計の値からきています.
1年に1回利息を元金に組み入れると,1年後の元利合計は 1*(1 + 1)^1
半年に1回利息を元金に組み入れると,1年後の元利合計は 1*(1 +1/2)^2
半年複利のために金利は1/2になります.以下同様です.
1月に1回利息を元金に組み入れると,1年後の元利合計は 1*(1 +1/12)^12
1日に1回利息を元金に組み入れると,1年後の元利合計は
1*(1 +1/365)^365
1年に1000回利息を元金に組み入れると,1年後の元利合計は
1*(1+1/1000)^1000
一般に,1年にn 回利息を元金に組み入れると,1年後の元利合計は
1*(1 +1/n)^n となります.
複利の計算からわかるように,n の数をかなり大きくしていくと,元利合計の
値は限りなく大きくなっていくように感じますが,実はそうではなく上限があ
るのです.なぜなら金利の値は逆にどんどん小さくなっていくからです.結局,
ある一定値に近づいていきます.それが自然対数の底 e = 2.71828..なのです.
複利の回数をどんなに大きくしていっても1年後の元利合計は 2.71828 万円
を超えることはあり得ないのです.
1
lim (1 + ------- )^n = 2.71828 = e
n->∞ n
年利1(100%)でなく一般に年金利rで預金したとき,複利計算の間隔を年
1回から半年,月,週,日,...としだいに連続的に短くしていったときの
預金の元利合計の究極的な値は,次のように計算できます.
ここで,m = n/r とおくと,
r 1 1
(1 + ---- )^n = (1 + --------- )^n = (1 + --------- )^(m r)
n n/r m
r 1
lim (1 + ---- )^n = lim(( 1 + -----)^m)^r = e^r
n->∞ n n->∞ m
同じようにして,t年後には
r r
lim (1 + ---- )^(nt) = lim(( 1 + -----)^n)^t = e^(rt)
n->∞ n n->∞ n
一般に,A円を年利rの複利で預金した場合,t年後には元利合計は
A e^(rt)
で増加していきます.
複利の金利を経済成長率とみなせば,上の式はGDPの成長率を表していると読
み替えることができます.GDPの初期値をAとし,年成長率をrとすれば,GDP
は次の式に基づいて成長してきます.
A e^(rt)
■Mathematica での表記法と計算
10 を底とする常用対数は,Mathematicaでは,Log[10, x] で表現します.自
然対数はLog[E, x] ですが,通常は,Log[x]で表現します.
以下で太字の部分は Mathematica のプログラム部分です.
常用対数の例 Log[10, 100] -> 2
自然対数 Log[E, 9] = Log[9]
E(大文字)は自然対数の底の記号として使います.
Log[9] を実行すると,MathematicaはLog[9]と返します.これは
Mathematicaの性質としてまずは厳密解を計算するからです.数値解を表示す
るには,
N[Log[9]]
2.19722
小数点以下の桁数をもっと表示させたい場合は,
N[Log[9],17]
2.1972245773362194
全部で17桁表示になっています.
自然対数の底 e の計算をMathematicaで実験することができます.
TableForm[
Table[{x, N[(1 + 1/x)^x]}, {x, 1, 10}]
]
1 2.0
2 2.25
3 2.37037
4 2.44141
5 2.48832
6 2.52163
7 2.5465
8 2.56578
9 2.58117
10 2.59374
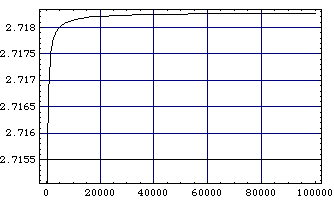
グラフで示すときは次のようにします.
Plot[
(1 + 1/x)^x, {x, 1, 100000},
GridLines -> Automatic,
Frame -> True
]

100万回計算すると,ちょっと時間がかかります.
N[1 (1 + 1/1000000)^1000000, 17]
答えは 2.7182804693193769
自然対数の底 e の意味を計算で確認すると次のようになります.
Limit[(1 + 1/n)^n, n -> Infinity]
答えは E
Limit[(1 + r/n)^n, n -> ∞]
答えは E^r
Limit[(1 + r/n)^(n t), n -> ∞]
答えは E^(r t)
■参考文献
Simon, Carl P.and Blume, Lawrence(1994), Mathematics for Economists,
W W Norton. Chapter 5 Exponents and Logarithms
中級レベルの経済数学のテキストとして定評があるものです.
■高校数学を復習するサイト
数学トレーニング講座:
http://www.geocities.co.jp/Technopolis-Mars/5427/mathtrtop.html
高校数学を復習するには最適のサイトです.この中の「指数・対数」の部分を
読んでください.
数学思い出コラム:
http://www.asahi-net.or.jp/~tt9h-hskw/sugaku/
この中に「対数コラム(1)常用対数が生活で利用されている例」
「対数コラム(2)自然対数の底 e はどこから出た」があります.
■まとめ------------
・高校数学では,10を底とする常用対数を学んだが,大学の経済学で重要なの
は e を底とする自然対数.
・e =約2.7182 の無理数.
・e とは,1万円を年利率1(100%)の複利で預金したときの元利合計の計算
で,複利回数を連続的に無限大に大きくしていったときの究極的な値.
・A円を年利rの複利で預金した場合,t年後の連続方式の元利合計は A e^(rt)
・GDPの初期値をAとし,年成長率をrとすれば,GDPのt年後の値は A e^(rt)
-------------------------------------
(注意)後日サイトにアクセスした場合,サイトの構成に違いがでてきたり,
URLが変更になっている場合がありますので,了解してください.
(アクセス日)2004年6月4日
------------------------------------------------------------
【Q & A】自然対数の底 e の値はおよそ?
→ 2.7182
【今回のサイト】 数学トレーニング講座:
http://www.geocities.co.jp/Technopolis-Mars/5427/mathtrtop.html
【評価】★★★
私の評価の基準:最高が★★★,次が★★,最後が★です.
★1つは普通という評価です.
データが十分提供されているかどうかが評価のポイントです.
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
【国経館アーカイブ】 http://groups.yahoo.co.jp/group/kokkeikan/
------------------------------------------------------------
【発行】 熊本学園大学 経済学部 国際経済学科
【著者】 笹山 茂
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
Copyright 2004