最近号のメールマガジン
第69回 経済数学の基礎(ミクロ経済学編) 最大・最小化問題[top]
2003年12月16日更新
2003年12月12日発行
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
国経館 経済数学の基礎 ミクロ経済学編 メールマガジン No.131
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
みなさん,こんにちは.笹山です.
このメールマガジンは国際経済学科のメールマガジン「国経館」の1つとして,
国際経済学科のすべての学生に配信されています.
今回は,ミクロ経済学で登場する経済数学の紹介です.
マクロ経済学のメールマガジンとしてはNo.69です.
------------------------------------------------------------
【第131号】 経済数学の基礎 ミクロ経済学編 最大・最小化問題
------------------------------------------------------------
経済学部の学生あるいは経済学部の卒業生には一般的にどのようなことが社会
から期待されていると思いますか? 法学部の学生なら法律の知識,経済学部
の学生なら経済の知識ということになるでしょうが,じゃあ,具体的に経済の
知識,経済学の知識とはなんでしょうか.
小野・中山・福田・本多編(2003)『現代経済学の潮流2003』東洋経
済新報社,の中の対談「経済学教育の実践的課題(パネルディスカッション)」
で,ある実務家は次のように述べています.
「我々の立場から見ると,数学のできない経済学部生というのは,結局,商品
性がない.それなら,法律を少しでも知っていたほうがいいという感じになり
ます.もともと経済学部にも,金融を勉強している人やマイクロを勉強してい
る人など,いろいろな人がいるわけですが,おそらく数学と基本的な統計学と
基本的なマイクロの考え方みたいなのが最も基本で,そこがきちんとしていれ
ば,「自分自身の直面する問題を実際に分析してみなさい.データはこれです」
という形でやっていけば,あとは実は何とかなるということです(同書244
−245ページから引用).」
この方は,要するに経済学部生が学ぶべき基本として数学(経済数学),統計
学,マイクロ(ミクロ経済学のこと)の3つを挙げているのです.
わたしなら,上の3つに,さらにマクロ経済学,計量経済学(コンピュータに
よるデータ処理)を必須科目として付け加えます.
ものごとを論理的に考える,数理的に処理できるという能力は経済学を学んで
いく過程で徐々に身に付いていきます.みなさんも1年次のマクロ経済学,ミ
クロ経済学で十分であると思うことなく(はっきりいってマクロ1,ミクロ1
だけでは不十分です),2年次以上に開設してあるマクロ経済学2,ミクロ経
済学2,計量経済学をぜひ履修してください.
そういうわけで,今回は経済学の中でもコア科目の1つであるミクロ経済学
(microeconomics英語ではマイクロエコノミクスと発音)で頻繁に登場する
経済数学の中から,最大・最小(極大・極小ともいいます)問題を例題を示し
ながら紹介します.
以下で★がついている項目は上級者向けですので,1年生のみなさんは飛ばし
て読んでください.もちろん,数学が得意な学生はチャレンジしてください.
また,☆で Mathematica を用いた解答も紹介しておきます.こちらも参考に
してください.Mathematica については,私のメールマガジン「Mathematica
のススメ」を参照してください.
メールマガジン Mathematica のススメ:
http://www.kumagaku.ac.jp/teacher/~sasayama/macroecon/mailmagamath.html
■最大・最小化問題を解く
最大・最小化問題には大きく分けて2つあります.1つは制約条件のない最大
・最小問題であり,もう1つは制約条件付きの最大・最小問題です.まずは簡
単な制約条件のない問題から始めましょう.
1年次向けの入門ミクロ経済学では原則として微分・積分は使わないで説明す
ることになっていますが,部分的に微分を使った解き方も紹介しています.
ミクロ経済学2やマクロ経済学2では本格的に微積分が登場します.2年生に
なったら微積分もそろそろ学び始めた方がいいでしょう.公務員試験を目指し
ている学生も多くいるかと思いますが,はっきり言って,微積分ができないと
公務員試験にでてくるマクロ,ミクロの問題は解けません.これだけはしっか
り覚えておいてください.
【例題1】企業の利潤極大化------------------------------------
ある企業の生産関数が Q=X^0.5で表されています.Qは生産物の量,
Xは生産要素労働の量であり,要素価格(賃金)は0.25です.この生産物
の価格は1とします.このとき,この企業の利潤が最大となるときの労働投入
量Xを求めなさい.
-----------------------------------------------------------
(例題1の解説)
最初は制約条件のない最大化問題です.
利潤=売上−費用 です.ここでは生産物はすべて販売されるものと想定しま
す.利潤はπ(パイ)という記号を使います.与えられた条件から利潤を定義
すると,
π = 1*x^0.5 - 0.25*x (1)
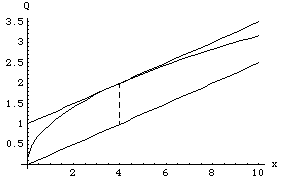
横軸にx,縦軸にQをとった図を描くと,利潤が最大となるのは,生産関数の
接線と費用線の傾きが等しくなるときです.

生産関数 x^0.5をx で微分すると,0.5 x^(-0.5)です.
結局,利潤最大の条件は,
0.5 x^(-0.5) = 0.25
これから,x = 4
(答)x=4
☆ Mathematica program --------------
rijun = x^0.5 - 0.25*x;
kai = Solve[D[rijun, x] == 0, x]
------------------------------------
(プログラム解説)
Solve は方程式を解く関数です.
== は Mathematica では方程式の等号です.
= は右辺を左辺に置くという意味だけをもちます.
Dは偏微分の関数です.
Mathematica では関数の頭文字は必ず大文字にします.
【例題2】所得制約のもとでの効用最大化---------------------------
ある合理的な消費者の効用関数が,U = X・Y (X:X財の消費量,Y:Y財の
消費量)で示されるとします.この消費者は当初,X財を20個,Y財を20
個所有しているとします.この消費者が効用を最大にするためにはX財とY財
をそれぞれどれだけ所有すればよいでしょうか.ただし,X財の価格2,Y財
の価格1で,この消費者は当初貨幣をまったくもっていないものとします.
------------------------------------------------------------
(例題2の解説)
この問題は典型的な「制約条件付きの最大化問題」です.この場合の制約条件
は所得あるいは予算の制約です.消費者は現在の所得の範囲内でみずからの
「効用」を最大にするX財とY財の所有の組み合わせを求めます.
初期の所得は,X財を20個,Y財を20個もっているので,それぞれの価格
をかけると求まります.
20×2 + 20×1 = 60
効用関数 U = X・Y (1)
予算制約式 60 = 2*X + Y (2)
予算制約条件を効用関数に代入して,Uが最大となるときのXを求めます.
(2)から, Y = 60 - 2*X を(1)に代入します.
U = - 2 x^2 + 60*x = - 2 { (x - 15)^2 - 225} (3)
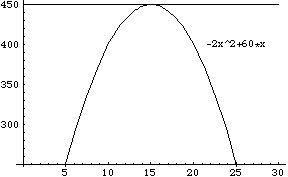
UはXの2次関数になるので,上のように変形することができます.(3)式
は上向きに凸の放物線になっています.結局(3)から,U はX = 15 のとき
最大となります.
X = 15 を予算制約式(2)に代入するとYが求まります.
Y = 60 - 2*15 = 30
この消費者にとって,効用を最大にする消費の組み合わせは X = 15, Y = 30
となります.
(答)X = 15, Y = 30
★(上級者向け)
制約条件付の最大・最小化問題を解く場合は,ラグランジュ未定係数法を使い
ます.
(注)ラグランジュ未定係数法は経済学部の上級生(3,4年生)にとっては
必須事項です.
問題設定:
max U = X・Y (目的関数)
s.t. 60 = 2*X + Y (制約条件)
(注:max A s.t. B はBの制約のもとでsubject to,Aをmaximizeすると
いう意味です.)
ラグランジュ未定係数法を使うと,上の問題は次のように書くことができます.
L = X・Y + λ(60 - 2*X - Y) (4)
λがラグランジュ乗数,Lがラグランジュ関数です.
最大化条件は次の3つの条件で示されます.最適化の1階の条件(first order
condition)と呼んでいます.Lを変数X,Y,λでそれぞれ偏微分した値をゼロ
とおきます.偏微分=0で最大の条件が求まるのです.偏微分を計算すること
は関数のある点での傾きを求めることと同じなので,その傾き=0というのは
その点は極値,すなわち最大点になります.
dL
---- = Y - 2*λ = 0 (5)
dX
dL
---- = X - λ = 0 (6)
dY
dL
---- = 60 - 2*X - Y = 0 (7)
dλ
上の3つの式(5)〜(7)から,X = 15,Y = 30 が得られます.
(注)上の式でdL/dX等の部分が微分です.LをXで偏微分しています.dは本来
は偏微分記号のラウンドを使います.
☆ Mathematica program --------------
Clear[f, g, L, x, y, lambda];
f[x_, y_] := x*y;
g[x_, y_] := 60 - 2*x - y;
L[x_, y_, lambda_] := f[x, y] + lambda*g[x, y];
c = Solve[
{
D[L[x, y, lambda], x] == 0,
D[L[x, y, lambda], y] == 0,
D[L[x, y, lambda], lambda] == 0
}, {x, y, lambda}
]
------------------------------------------------
(プログラム解説)
f[x_, y_] := は関数定義です.
Clear は変数のメモリを消去します.
【例題3】生産量の下で費用最小化--------------------------------
要素市場が完全競争にあるとき,ある企業の生産関数が,生産量Q,資本スト
ックK,労働力Nとして,Q=2K・N で与えられています.いま,生産量
Q=100が計画され,要素価格がKについて1万円,Nについて2万円であ
るとき,費用を最小にするKとNの最適投入量の組み合わせを求めなさい.
------------------------------------------------------------
(例題3の解説)
この問題を高校数学の延長で解く場合は,数学2で学ぶ「接線の傾き」の知識
が必要となります.
(接線の傾き)=======================================
曲線 y = f(x) 上の点A(a, f(a))における接線の傾きは,
微分係数 f'(a) に等しい.
あるいは,曲線 y = f(x) 上の点A(a, f(a))での接線の方程式は,
y - f(a) = f'(a)(x - a)
である.
===================================================
生産量100の場合の生産関数は, 100=2K・N (1)
費用をCで表すと, C=1K+2N (2)
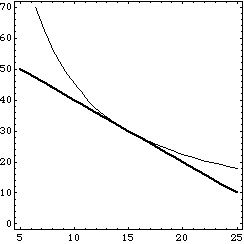
横軸にN(労働),縦軸にK(資本)をとった図を描くと,生産関数(あるい
は等量曲線)は双曲線であり,費用線は右下がりの直線になります.
費用が最小となるのは,費用線が生産関数に接するときです.双曲線(生産関
数,ここでは等量曲線)と費用線が接する条件は次のようになります.
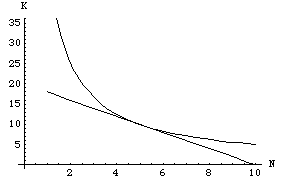
費用線の傾き=等量曲線の接線の傾き (3)
費用線の傾きは,(2)式から−2であることがすぐわかります.
等量曲線の接線の傾きは,(1)から,
K=50/N (4)
と変形して,Nについて微分します.これで接線の傾きが求められます(上の
接線の公式参照).
(4)をNについて微分すると(このとき商の微分の公式*を使います),
−50/N^2
従って,(3)の条件は,
−2 = −50/N^2
これから, N=5 がえられます.N=5を(1)に代入すると,Kが求ま
ります. K=10
(答)N=5,K=10
(注*)商の微分の公式------------
y 1
d(-----) = --------(x・dy−y・dx)
x x^2
-----------------------------------------------
★(上級者向け)ラグランジュ未定係数法による解法
問題設定:
min K + 2*N (目的関数)
s.t. 100 = 2K*N (制約条件)
ラグランジュ未定係数法を使うと,上の問題は次のように書くことができます.
L = K + 2*N + λ(100 - 2*K*N) (5)
λがラグランジュ乗数です.
最小化の1階の条件は以下になります.
dL
---- = 1 - 2*N*λ = 0 (6)
dK
dL
---- = 2 - 2*K*λ = 0 (7)
dN
dL
---- = 100 - 2*K*N = 0 (8)
dλ
上の3つの式(6)〜(8)から,N = 5,K = 10 が得られます.
☆ Mathematica program --------------
Clear[f, g, L, x, y, lambda];
f[x_, y_] := x + 2*y;
g[x_, y_] := 100 - 2*x*y;
L[x_, y_, lambda_] := f[x, y] + lambda*g[x, y];
c = Solve[
{
D[L[x, y, lambda], x] == 0,
D[L[x, y, lambda], y] == 0,
D[L[x, y, lambda], lambda] == 0
}, {x, y, lambda}
]
------------------------------------------------
(注)上で,x = K,y = Nです.Mathematica では N は数値解をえる関数と
してすでに決まっているので,利用者は自分のプログラム内で N を使えません.
■前提となる高校数学の知識
・2次関数,放物線の性質
・2次関数の最大,最小
・接線の傾き,あるいは,接線の公式
・基礎的な微分の計算(積と商の微分)
■関連サイト紹介
数学ナビゲーター 数学2:
http://www.crossroad.jp/mathnavi/math-ii/math-ii-index.html
高校数学の復習サイトとして利用してください.
ミクロ経済学講義ノート(法政大学 奥山利幸先生):
http://okuyama.mt.tama.hosei.ac.jp/education/microeconomics/
ミクロ経済学問題集(ミクロ経済学の間):
http://www2.nasicnet.com/~tell-g/monndai.html
★経済数学入門(PukiWiki):
http://www.matsusaka-u.ac.jp/~aihara/pukiwiki2/index.php?
関数,微積分,微分方程式までカバーしています.
■参考文献
小野善康・中山幹夫・福田慎一・本多佑三,編(2003)
『現代経済学の潮流2003』東洋経済新報社.
第8章 経済学教育の実践的課題(パネルディスカッション)
宇沢弘文(2001)『好きになる数学入門5 関数を調べる 微分法』岩波書店
微分の基本的な概念から丁寧に説明してくれます.ラグランジュ未定係数法は
第9章で登場します.
宇沢弘文(1990)『経済解析 基礎編』岩波書店
ラグランジュ未定係数法は第16章で解説しています.
浅利一郎・山下隆之(2003)『はじめよう経済数学』日本評論社
最初に高校数学の復習を整理してあります.
ディキシット(1997)『経済理論における最適化』勁草書房
西村清彦(1990)『経済学のための最適化理論入門』東京大学出版会
これは上級者向けです.
Huang C.J. and P.S. Crooke(1997), Mathematics and Mathematica
for Economists, Blackwell.
経済数学と Mathematica について参考になります.上のプログラムはこの本を参考にしています.
公務員受験向けの演習書としては以下があります.いずれも豊富な練習問題
が載っています.
西村和雄(1990)『入門経済学ゼミナール』実務教育出版
原田泰(1996)『経済学スーパー解法テクニック』実務教育出版
資格試験研究会編(2000)『公務員試験スーパー過去問ゼミ ミクロ経済学』実務教育出版
■まとめ------------
・経済学部生にとって,数的な考え方,論理的な思考方法が重要である.
・ミクロ経済学,マクロ経済学,経済数学,統計学,計量経済学はぜひ履修しておこう.
・ミクロ経済学では,最大・最小化問題を理解することが1つのキーである.
・最大・最小化問題には,制約条件付きと制約条件なしの2タイプがある.
・関数の極値(最大値,最小値)での接線の傾きはゼロである.
・接線の傾き=0を数学で表現すれば,関数の偏微分=0
・上級者は,ラグランジュ未定係数法をぜひマスターしよう.
-------------------------------------
(注意)後日サイトにアクセスした場合,サイトの構成に違いがでてきたり,
URLが変更になっている場合がありますので,了解してください.
(アクセス日)2003年12月12日
------------------------------------------------------------
【Q & A】関数の極値(最大値,最小値)での接線の傾きの大きさは?
→ ゼロ
【今回のサイト】 経済数学入門(PukiWiki):
http://www.matsusaka-u.ac.jp/~aihara/pukiwiki2/index.php?
【評価】★★★
私の評価の基準:最高が★★★,次が★★,最後が★です.
★1つは普通という評価です.
データが十分提供されているかどうかが評価のポイントです.
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
【発行】 熊本学園大学 経済学部 国際経済学科
【著者】 笹山 茂
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
Copyright 2003