45度線との交点が均衡所得を表します.
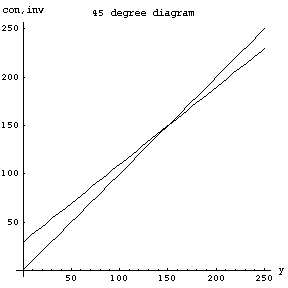
最近号のメールマガジン
第67回 Mathematica のススメ[top]
2004年2月10日更新
2003年11月28日発行
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
国経館 Mathematica のススメ メールマガジン No.128
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
みなさん,こんにちは.笹山です.
このメールマガジンは国際経済学科のメールマガジン「国経館」の1つとして,
国際経済学科のすべての学生に配信されています.
今回は,便利なソフトウェアの紹介です.
マクロ経済学のメールマガジンとしてはNo.67です.
------------------------------------------------------------
【第128号】 Mathematica のススメ
------------------------------------------------------------
データを扱うコンピュータ用のソフトウェアとしてみなさんがすぐ思いつくの
はエクセルでしょう.国際経済学科の1年生用必修科目「情報処理入門」でも
エクセルの基礎的な使い方を学んだことと思います.エクセルではまず数値が
ないと先へは進めません.数値を与えてやれば,それをもとにして伸び率や平
均を計算したり,さらにはそれらのデータを様々なグラフに表示することもで
きます.エクセルは経済学部の学生にとってなくてはならない分析道具になっ
ています.
その一方,経済学では理論を説明するときは記号を使います.1年生でまず最
初に学ぶ簡単なGDP決定のマクロ経済モデルは次のように記述します.
財市場の均衡式 Y=C+I (1)
消費関数 C=Co + c*Y (2)
投資 I=Io (3)
ここで,Y:GDP, C:消費, Co:基礎消費,c:限界消費性向,
I:投資, Io:最初に与えられた投資.oがついているのはモデルの外から
与えられた定数です.
上の3本の式から,計画された段階で供給=需要をみたす所得水準(均衡所得)
を求めるには,(2)と(3)を(1)に代入してYについて解くという手順
を踏みます.
記号のまま式を展開して解答を得るというような問題にエクセルを使うことは
できません.エクセルで答えを求めようとするには,それぞれの式に具体的な
数値を与えてやらなければなりません.
今回紹介するソフトウェアMathematica(マセマティカ)は,実は上で示した
ような記号のままで式を扱い,答をだしてくれるという”優れもの”なのです.
記号をそのまま扱えるというので「数式処理ソフトウェア」と呼ばれています.
■Mathematicaとは
Mathematicaは名前からも想像できるように本来は数学用のソフトウェアです.
しかし,数式やデータを使う分野ならどのような分野にも活用できます.
Mathematicaを使うとどのようなことができるかを経済学の分野に絞って紹介
しておきましょう.
●(例その1)方程式を解く
1本の方程式でも,連立方程式でも解くことができます.最初に紹介した簡単
なマクロモデルは連立方程式とみなして解くことができます.Mathematicaで
記述したプログラムを紹介しておきましょう.
-----この線ではさまれた太字部分がプログラムです(以下同様)---
(* simple macro model *)
model = {
y== con + inv,
con == con0 + mpc y,
inv == inv0
};
kai = Solve[model, {con, inv, y}]
kai /. {con0 -> 10, inv0 -> 20, mpc -> 0.8}
-----この線ではさまれた部分がプログラムです------------------
上のプログラムを実行すると,次のような解をだしてくれます.
con0 + inv0 mpc con0 + inv0
con -> - ----------------- , y -> - ------------- , inv
-> inv0
- 1 + mpc - 1 + mpc
{{con -> 130., y -> 150., inv -> 20}}
(プログラムの解説)----------
3本の方程式を model という名前で定義して,このmodelを con,inv,yの3
変数について解いています.方程式を解く関数は Solve です.
さらに,con0に10,inv0に20,mpc(限界消費性向)に0.8を代入すると,数値
解も求めてくれます.
----------------------------------------------------------
Mathematicaの記号の規則から,われわれが経済学でよく使う記号のCやIは
使えないので上のように書いています.Cは定数項として,Iは虚数単位とし
てMathematicaが使うことになっているのです.このあたりはMathematicaを初
めて使う人にとっては戸惑うことかもしれません.
上の例は非常に簡単な連立方程式なのであえてMathematicaを使うほどではな
いのですが,Mathematicaのありがたさがわかるのはもっと多くの式からなる
連立方程式体系を解くときです.
Mathematicaは計算するだけでなく,すぐれたグラフィックス機能も持ってい
ます.計算結果をグラフに表示することも簡単にできます.マクロ経済学の初
めの段階で登場する45度線図も容易に描いてくれます.次のようなプログラ
ムです.
-----45度線図のプログラム--------------------
(* 45 degree diagram *)
con0 = 10;
inv0 = 20;
mpc = 0.8;
(*define demand function*)
dm[y_] := con0 + inv0 + mpc y;
(* plot demand and 45 degree line *)
Plot[
{dm[y], y}, {y, 0, 250},
AspectRatio -> Automatic,
AxesLabel -> {"y", "con,inv"},
PlotLabel -> "45 degree diagram"
]
-----------------------------------------------
上を実行すると,おなじみの45度線図が現れます(下図).
45度線との交点が均衡所得を表します.
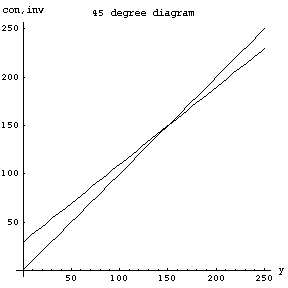
●(例その2)生産関数のグラフ
Mathematicaは3次元の図を描くのも得意です.次のプログラムは経済学の分
野では非常に有名なコブ・ダグラス型生産関数を3次元の図として描いたもの
です.その後,水平面で輪切りにした図を出力します.この図がミクロ経済学
の生産のところで登場する等量曲線になります.
---コブ・ダグラス型生産関数(一次同次)----------------------------
z = 60 x^0.6 y^0.4
g = Plot3D[z, {x, 0, 10}, {y, 0, 10}, ViewPoint -> {-1, -3,
0.7}]
ContourPlot[z, {x, 0, 10}, {y, 0, 10}, PlotPoints -> 30]
--------------------------------------------------------------------
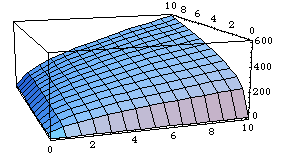
上を実行すると一次同次のコブ・ダグラス型生産関数の3D図が現れます.
一次同次の生産関数とは,すべての生産要素(上では資本と労働)を例えば2倍
に増やせば,生み出される生産量も2倍になるタイプの生産関数のことです.
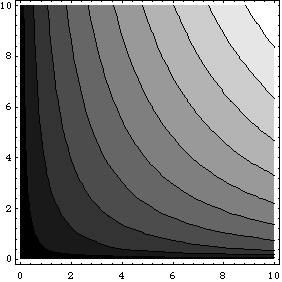
下図は,上の生産関数を輪切りにした等高線図である「等量曲線」です.
●(例その3)回帰分析(regression)の例
以下には基本的な回帰分析のプログラムを掲載しておきました.ちょっと長い
ですが,コピーアンドペーストすれば Mathematica へ簡単にもっていけます.
推定する消費関数の形は次です.
Y= a + b* X
消費=切片+傾き*所得
Needs["Statistics`LinearRegression`"]; で回帰分析用のプログラムを呼び
出します.後で,複数のデータを同時にグラフにする必要がありますで,
Needs["Graphics`MultipleListPlot`"]も実行しておきます.Needs["Graphics`Legend`"]
はグラフに凡例(はんれい)を表示するために必要です.
データの入力は,必ず{X軸(横軸,説明変数)のデータ,Y軸(縦軸,被説明変数)
のデータ}の順に並べます.消費関数の場合,Xは所得,Yは消費になります.データ
は22個あります.全体を{ } でくくります.これをリスト形式のデータと呼んでいます.
(注)以下のプログラムで (* *) で囲んである部分は注釈文です.Mathematica
はこの部分は無視して実行します.
---回帰分析のプログラム(単純回帰)----------------------------
(*** 事前に読み込んでおくパッケージ ***)
Needs["Statistics`LinearRegression`"];
Needs["Graphics`MultipleListPlot`"];
Needs["Graphics`Legend`"];
(*** 回帰分析用のデータ ***)
data = {{66.0,56.6},{72.0,62.3},{79.9,68.2},
{87.4,74.7},{97.1,81.9},{107.3,87.4},
{111.8,92.8},{124.6,102.6},{136.1,109.1},
{143.6,110.5},{149.1,114.7},{153.7,119.3},
{158.3,124},{163.9,131.8},{167.8,138.5},
{170.3,139.7},{173.4,142.4},{176.8,148.6},
{182.4,152.9},{186.6,156.8},{191.9,161.1},
{199.5,166.9}};
(*** XとYの散布図を描く ***)
scatter = ListPlot[data,
AxesLabel -> {"X", "Y"},
PlotLabel -> "Scatter Diagram";
(*** 回帰分析の基本プログラム部分 ***)
kaiki = Regress[data,{1,x},x,
RegressionReport ->
{ParameterTable,
ANOVATable,
EstimatedVariance,
RSquared,
AdjustedRSquared,
DurbinWatsonD,
FitResiduals,
SinglePredictionCITable,
ParameterConfidenceRegion}]
(*** 回帰式だけを求める ***)
func = Fit[data,{1,x},x]
(*** 推定の標準誤差を計算 ***)
RSS = EstimatedVariance /. kaiki;
SE = Sqrt[RSS];
Print["Standard Error = ", SE];
(*** 観測値,予測値,残差のデータを取り出す ***)
errors = FitResiduals /. kaiki;
{observed, predicted, se, ci} =
Transpose[(SinglePredictionCITable /. kaiki)[[1]]];
(*** 観測値,予測値,残差をグラフに描く ***)
MultipleListPlot[observed, predicted,
PlotJoined -> {False, True},
PlotLabel -> "Observed vs Predicted";
ListPlot[errors,
PlotJoined -> True,
PlotLabel -> "Residuals";
(*** 信頼区間をグラフに描く ***)
(xval=Map[First,data];
predicted=Transpose[{xval,predicted}];
lowerCI=Transpose[{xval,Map[First,ci]}];
upperCI=Transpose[{xval,Map[Last,ci]}]);
MultipleListPlot[
data,predicted,lowerCI,upperCI,
SymbolShape -> {PlotSymbol[Diamond],None,None,None},
PlotJoined -> {False,True,True,True},
PlotStyle -> {Automatic,Automatic,Dashing[{.05,.05}],
Dashing[{.05,.05}]},
PlotLabel -> "Confidence Interval",
AxesLabel -> {"X","Y"}
]
(*** 残差の自己相関をグラフに描く ***)
zansa1 = Take[errors, n - 1]
zansa2 = Take[errors, {2, n}]
zansapair = {zansa1, zansa2}
zansajikosokan = Transpose[zansapair]
ListPlot[zansajikosokan,
AxesLabel -> {"ut-1", "ut"},
PlotStyle -> PointSize[0.02],
PlotLabel -> "Autocorrelations of Residuals";
--------------------------------------------------------------------
今回は3つの応用例だけを紹介しましたが,経済学の様々な分野に応用できます.
・金融計算
・時系列分析
・微分・積分
・微分方程式
・定差方程式
その他にも応用できます.
ぜひ,みなさんも機会があったらMathematicaに触れてみてください.
■Mathematica 関連サイト
★Wolfram Research社:
http://www.wolfram.com/
Mathematicaを開発している会社のサイトです.必須サイトです.
★Mathematica 4 ドキュメント:
http://documents.wolfram.com/v4-ja/index.html
Mathematica のオンラインマニュアルです.
Mathematica Information Center:
http://library.wolfram.com/infocenter
MathSource:
http://library.wolfram.com/infocenter/MathSource
MathWire:
http://www.wolfram.com/news/mathwire/
Eric Weistein's World of Mathematics:
http://mathworld.wolfram.com/
Mathematica Journal:
http://www.mathematica-journal.com/
Mathematicaレファレンスマニュアル:
http://www.aerith.net/project/Mathematica-j.html
Mathematicaの関数の解説が整理されています.
Ohgi's PukiWiki:
http://web.sfc.keio.ac.jp/~ohgi/
Mathematicaをスポーツ工学へ応用しています.
★Mathematica-Tips:
http://www.sigmath.es.osaka-u.ac.jp/~n-funao/mathematica/math.html
Mathematicaの使い方を例とともに紹介しています.
日本Mathematicaユーザ会:
http://www.jp-mathusers.org/
神戸大学 Mathematica ホームページ:
http://bach.istc.kobe-u.ac.jp/mma/
Mathematica 関連のリンク集もあります.
■Mathematica 参考図書
Mathematicaを経済関連分野に応用した文献を紹介します.
Varian, Hal R. ed.(1993), Economic and Financial Modeling
with Mathematica,
Springer-Verlag.
Varian, Hal R. ed.(1996), Computational Economics and Finance,
Springer-Verlag.
以上の2つは専門論文集です.
Abell, M.L. and J.P. Braselton(1993), Differential Equations
with Mathematica,
Academic Press.
微分方程式を解くとき参考になります.
Huang, C.J. and P.S. Crooke(1997), Mathematics and Mathematica
for Economists,
Blackwell.
Mathematica を活用した経済数学の図書です.
Shaw, William(1998), Modelling Financial Derivatives with
Mathematica,
Cambridge University Press.
デリバティブに関する専門書です.
Rose, C. and M.D. Smith(2002), Mathematical Statistics with Mathematica, Springer.
笹山 茂(1994)『マッキントッシュで経済学』日本評論社
小林道正(1994)『Mathematica 確率・統計入門』トッパン
中村健蔵(1996)『Mathematica によるOR』アジソン・ウェスレイ・パブリッシャーズ・ジャパン
小林道正(1996)『Mathematica による『ミクロ経済学』スタディガイド』東洋経済新報社
浅利・久保・石橋・山下(1997)『はじめよう経済学のためのMathematica』日本評論社
椎原浩輔(2000)『Mathematica による金融工学』東京電気大学出版局
吹原俊隆(2002)『Mathematica による経済数学入門』牧野書店
大川勉(2002)『コンピュータ金融工学入門』阿吽社
Mathematica の基礎を学ぶテキストとしては以下がよいでしょう.
榊原進(2000)『はやわかりMathematica 第2版』共立出版
Mathematicaの関数の使い方を知るには以下が便利です.ちょっと旧いですが.
N. ブラックマン著,榊原進監修,新井・川幡・松井訳(1994)『Mathematica事典』トッパン
Mathematica のオリジナル解説書は,開発者による次が基本です.かなり分厚い.
Wolfram, S.(2003), The Mathematica Book 5th Edition, Wolfram
Media.
■まとめ------------
・Mathematicaは記号をそのままの形で扱うことができるソフトウェアである.
・数式を扱う分野であれば,様々なところで応用可能.
・数式処理以外に,数値計算,グラフィックス機能も備えている.
・経済学の様々な分野に活用できる.
-------------------------------------
【課題】
本学の情報教育センターの第6と第7パソコン室ではMathematicaを利用でき
ます.今回紹介したプログラムを入力して,実行してみましょう.
プログラムを実行するには 小さなenterキーを押します.
(注意)後日サイトにアクセスした場合,サイトの構成に違いがでてきたり,
URLが変更になっている場合がありますので,了解してください.
(アクセス日)2003年11月28日
------------------------------------------------------------
【Q & A】Mathematicaはどのジャンルに所属するソフトウェア?
→ 数式処理ソフトウェア
【今回のサイト】 Wolfram Research社:
http://www.wolfram.com/
【評価】★★★
私の評価の基準:最高が★★★,次が★★,最後が★です.
★1つは普通という評価です.
データが十分提供されているかどうかが評価のポイントです.
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
【発行】 熊本学園大学 経済学部 国際経済学科
【著者】 笹山 茂
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
Copyright 2003